Коротко опишем фрагмент алгоритма сортировки с помощью прямого включения:
For k := 2 to n do
begin
x := a[k]; j := k-1;
{ вставить х на подходящее место в a[1], …, a[k] }
{ для этого организуем цикл, которые выполняется, пока }
{ j > 0 и x <= a[j] }
{в цикле смещаем элементы массива на 1 позицию вправо }
{по выходу из цикла вставляем х в позицию j+1массива }
end;
Контрольное задание
Написать программу вставки последнего элемента массива после первого отрицательного элемента этого же массива.
Варианты заданий
ВНИМАНИЕ!!! Если явно не указано иное, входные данные (исходный массив) и выходные данные (отсортированный массив) формировать в виде текстового файла, содержащего целые числа!
Для всех заданий предварительно написать процедуру сортировки массива методом прямого включения.
1. Дан ряд, содержащий n элементов. Отсортировать их в порядке возрастания, отбрасывая при этом все повторяющиеся элементы.
2. Определить моду данного ряда – значение, встречающееся среди его элементов чаще всего.
3. Исходный набор данных представляет собой последовательность записей, состоящих из фамилии, возраста и стажа работы. Распечатать этот список: 1) в алфавитном порядке; 2) в порядке увеличения возраста; 3) в порядке увеличения стажа работы.
4. Написать процедуру сортировки по убыванию.
5. Дан ряд целых чисел. Получить в порядке возрастания все различные числа, входящие в этот ряд.
6. Дан ряд из n различных целых чисел. Получить различные целые числа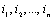 такие, что
такие, что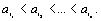 7. Даны целые
7. Даны целые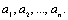 Найти наибольшее значение в этой последовательности после выбрасывания из нее всех членов со значением
Найти наибольшее значение в этой последовательности после выбрасывания из нее всех членов со значением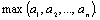 8. Даны натуральные
8. Даны натуральные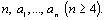 Числа
Числа 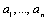 – это измеренные в сотых долях секунды результаты n спортсменов в беге на 100 м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100, т. е. указать одну из четверок натуральных чисел i, j, k, l такую, что сумма
– это измеренные в сотых долях секунды результаты n спортсменов в беге на 100 м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100, т. е. указать одну из четверок натуральных чисел i, j, k, l такую, что сумма 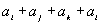 имеет наименьшее значение.
9. Дано n независимых случайных точек, с координатами (xi; yi), равномерно распределенных в круге радиуса 1 с центром в начале координат. Напишите программу, располагающую точки в порядке возрастания расстояния от центра.
10. Даны n целых положительных двузначных чисел. Трактуя каждое число как пару цифр из интервала 0–9, отсортировать их (цифры) по возрастанию.
11. Дано n точек на плоскости. Указать (n-1)-звенную несамопересекающуюся замкнутую ломаную, проходящую через все эти точки. (Соседним отрезкам ломаной разрешается лежать на одной прямой.)
Подсказка. Возьмем самую левую точку (т.е. точку с наименьшей x-координатой) и проведем из нее лучи во все остальные точки. Теперь упорядочим эти лучи снизу вверх, а точки на одном луче упорядочим по расстоянию от начала луча (это делается для всех лучей, кроме нижнего и верхнего). Ломаная выходит из выбранной (самой левой) точки по нижнему лучу, затем по всем остальным лучам (в описанном порядке) и возвращается по верхнему лучу.
12. Дано n точек на плоскости. Построить их выпуклую оболочку - минимальную выпуклую фигуру, их содержащую. (Резиновое колечко, натянутое на вбитые в доску гвозди - их выпуклая оболочка.)
Указание. Упорядочим точки. Затем, рассматривая точки по очереди, будем строить выпуклую оболочку уже рассмотренных точек.
имеет наименьшее значение.
9. Дано n независимых случайных точек, с координатами (xi; yi), равномерно распределенных в круге радиуса 1 с центром в начале координат. Напишите программу, располагающую точки в порядке возрастания расстояния от центра.
10. Даны n целых положительных двузначных чисел. Трактуя каждое число как пару цифр из интервала 0–9, отсортировать их (цифры) по возрастанию.
11. Дано n точек на плоскости. Указать (n-1)-звенную несамопересекающуюся замкнутую ломаную, проходящую через все эти точки. (Соседним отрезкам ломаной разрешается лежать на одной прямой.)
Подсказка. Возьмем самую левую точку (т.е. точку с наименьшей x-координатой) и проведем из нее лучи во все остальные точки. Теперь упорядочим эти лучи снизу вверх, а точки на одном луче упорядочим по расстоянию от начала луча (это делается для всех лучей, кроме нижнего и верхнего). Ломаная выходит из выбранной (самой левой) точки по нижнему лучу, затем по всем остальным лучам (в описанном порядке) и возвращается по верхнему лучу.
12. Дано n точек на плоскости. Построить их выпуклую оболочку - минимальную выпуклую фигуру, их содержащую. (Резиновое колечко, натянутое на вбитые в доску гвозди - их выпуклая оболочка.)
Указание. Упорядочим точки. Затем, рассматривая точки по очереди, будем строить выпуклую оболочку уже рассмотренных точек.
Назад
На главную
Нет комментариев.
Оставить комментарий:
|
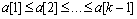 . Далее необходимо взять k-й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое
. Далее необходимо взять k-й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое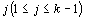 что
что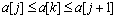 . Затем надо вставить элемент a[k] на найденное место.
. Затем надо вставить элемент a[k] на найденное место.
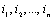 такие, что
такие, что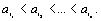
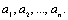 Найти наибольшее значение в этой последовательности после выбрасывания из нее всех членов со значением
Найти наибольшее значение в этой последовательности после выбрасывания из нее всех членов со значением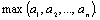
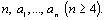 Числа
Числа 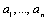 – это измеренные в сотых долях секунды результаты n спортсменов в беге на 100 м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100, т. е. указать одну из четверок натуральных чисел i, j, k, l такую, что сумма
– это измеренные в сотых долях секунды результаты n спортсменов в беге на 100 м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100, т. е. указать одну из четверок натуральных чисел i, j, k, l такую, что сумма 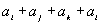 имеет наименьшее значение.
имеет наименьшее значение.