Лабораторная работа №4
Бинарный поиск
Общие сведения
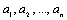 –целочисленный массив и
–целочисленный массив и 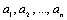 ; b – целое число. Рассмотрим задачу: выяснить, входит ли данное число в массив
; b – целое число. Рассмотрим задачу: выяснить, входит ли данное число в массив 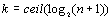 и если входит, то каково значение p, для которого ap = b? Эту задачу мы назовем задачей поиска элемента.
и если входит, то каково значение p, для которого ap = b? Эту задачу мы назовем задачей поиска элемента.
Пример
Пусть b = 6, а массив а состоит из 10 элементов: 3 5 6 8 12 15 17 18 20 25.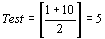 (Low=1, High=10). Так как 6
(Low=1, High=10). Так как 6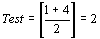 (Low=1, High=4). 6>a[2], следовательно, первый и второй элементы из рассмотрения исключаем:
3 5 6 8 12 15 17 18 20 25.
(Low=1, High=4). 6>a[2], следовательно, первый и второй элементы из рассмотрения исключаем:
3 5 6 8 12 15 17 18 20 25.
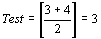 (Low=3, High=4):
3 5 6 8 12 15 17 18 20 25.
a[3] = 6! Элемент найден, его номер – 3.
(Low=3, High=4):
3 5 6 8 12 15 17 18 20 25.
a[3] = 6! Элемент найден, его номер – 3.
Контрольные вопросы
Варианты заданий
Для всех вариантов предварительно написать процедуру поискаУчебник по языку Pascal Лабораторные работы по программированию Справочник
Нет комментариев. Оставить комментарий: |