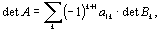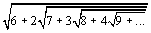Решение. Предположим, что мы умеем перекладывать пирамиду из (n-1) диска. Рассмотрим пирамиду из n дисков. Переместим первые (n-1) дисков на стержень С (это мы умеем). Затем перенесем последний n-й диск со стержня А на стержень В. Далее перенесем пирамиду из (n-1) диска со стержня С на стержень В. Так как n-й диск самый большой, то условие задачи не будет нарушено. Таким образом, вся пирамида будет на стержне В. Аналогичным образом можно перенести n – 2, n – 3 и т. д. дисков. Когда n=1, осуществить перенос очень просто: непосредственно с первого стержня на второй. При этом для решения задачи будет достаточно 2n - 1 перекладываний.
Program Example_2;
Const k = 3;
Var a,b,c : Char;
Procedure Disk(n : Integer; a, b, c: Char);
Begin
if n>0 then
begin
Disk(n-1,a,c,b);
Writeln(‘Диск ‘,n, ’ c ‘, a,’->’, b);
Disk(n-1,c,b,a);
end;
End;
BEGIN
a := ‘A’; b := ‘B’; c := ‘C’;
Disk(k,a,b,c);
ReadLn;
END.
Контрольные вопросы
1. На чем основан рекурсивный метод программирования?
2. В чем разница между «циклическим» и «рекурсивным» способами определения? Какой элемент является обязательным в рекурсивном определении?
3. Что такое «фрейм активации»?
4. К каким последствиям приводит «рекурсивное зацикливание»?
5. Какое условие должно обязательно присутствовать в любой рекурсивной процедуре?
6. Что такое явная и косвенная рекурсии?
7. Дайте рекурсивное определение целой степени числа N.
Варианты заданий
1. Ввести последовательность чисел (окончание ввода – 0) и вывести их в обратной последовательности. Входные данные взять из текстового файла.
2. Используя команды write(x) лишь при x=0..9, написать рекурсивную программу печати десятичной записи целого положительного числа n.
3. Напишите рекурсивную функцию, которая возвращает среднее из n элементов массива чисел.
4. Найти первые N чисел Фибоначчи двумя способами: с помощью рекурсии и с помощью итерации. Сравнить эффективность алгоритмов.
5. Написать функцию сложения двух чисел, используя только прибавление единицы.
6. Написать функцию умножения двух чисел, используя только операцию сложения.
7. Вычислить сумму элементов одномерного массива.
8. Найти НОД (наибольший общий делитель) двух натуральных чисел.
9. Вычислить несколько значений функции Аккермана для неотрицательных чисел m и n: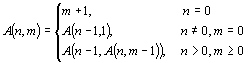 10. Напишите рекурсивную функцию, которая вычисляет длину строки.
11. Написать функцию C(m,n) вычисления биномиальных коэффициентов
10. Напишите рекурсивную функцию, которая вычисляет длину строки.
11. Написать функцию C(m,n) вычисления биномиальных коэффициентов 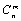 по следующей формуле:
по следующей формуле: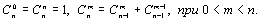 12. Проверить, является ли фрагмент строки с i-го по j-й символ палиндромом.
13. Вычислить произведение элементов одномерного массива.
14. Написать процедуру сортировки массива методом простого выбора.
15. Подсчитать количество цифр в заданном числе.
16. Написать функцию, проверяющую правильность имени в языке Pascal.
17. Написать функцию
12. Проверить, является ли фрагмент строки с i-го по j-й символ палиндромом.
13. Вычислить произведение элементов одномерного массива.
14. Написать процедуру сортировки массива методом простого выбора.
15. Подсчитать количество цифр в заданном числе.
16. Написать функцию, проверяющую правильность имени в языке Pascal.
17. Написать функцию 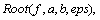 которая методом деления отрезка пополам (методом дихотомии) находит с точностью eps корень уравнения f(x) = 0 на отрезке [a,b] (
которая методом деления отрезка пополам (методом дихотомии) находит с точностью eps корень уравнения f(x) = 0 на отрезке [a,b] (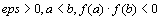 ). Метод дихотомии определяется следующим образом. Если f(a) и f(b) имеют разные знаки, то между точками a и b существует корень R. Пусть
). Метод дихотомии определяется следующим образом. Если f(a) и f(b) имеют разные знаки, то между точками a и b существует корень R. Пусть 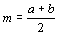 – средняя точка в интервале
– средняя точка в интервале 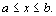 Если f(m) = 0, то корень R=m. Если нет, то либо f(a) и f(m) имеют разные знаки
Если f(m) = 0, то корень R=m. Если нет, то либо f(a) и f(m) имеют разные знаки 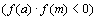 , либо f(m) и f(b) имеют разные знаки
, либо f(m) и f(b) имеют разные знаки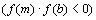 . Если
. Если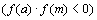 , то корень лежит в интервале
, то корень лежит в интервале 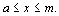 В противном случае он лежит в интервале
В противном случае он лежит в интервале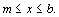 Теперь выполним это действие для нового интервала – половины исходного интервала. Процесс продолжается до тех пор, пока интервал не станет меньше eps.
18. В текстовом файле задана последовательность положительных чисел, за которой следует отрицательное число. Написать функцию без параметров для нахождения суммы этих положительных чисел.
19. Написать функцию без параметров, которая подсчитывает количество цифр в тексте, заданном в текстовом файле (за текстом следует точка).
20. Расстояния между городами заданы матрицей (Если между городами i,j есть прямой путь с расстоянием N, то элементы матрицы A(i,j) и A(j,i) содержат значение N, иначе 0). Написать программу поиска минимального пути для произвольной пары городов.
21. Вычислить определитель матрицы, пользуясь формулой разложения по первой строке:
Теперь выполним это действие для нового интервала – половины исходного интервала. Процесс продолжается до тех пор, пока интервал не станет меньше eps.
18. В текстовом файле задана последовательность положительных чисел, за которой следует отрицательное число. Написать функцию без параметров для нахождения суммы этих положительных чисел.
19. Написать функцию без параметров, которая подсчитывает количество цифр в тексте, заданном в текстовом файле (за текстом следует точка).
20. Расстояния между городами заданы матрицей (Если между городами i,j есть прямой путь с расстоянием N, то элементы матрицы A(i,j) и A(j,i) содержат значение N, иначе 0). Написать программу поиска минимального пути для произвольной пары городов.
21. Вычислить определитель матрицы, пользуясь формулой разложения по первой строке: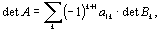 где матрица Bk получается из A вычеркиванием первой строки и k-го столбца.
22. Написать функцию определения, является ли заданное натуральное число простым.
23. Реализовать рекурсивный алгоритм построения цепочки из имеющегося набора костей домино.
24. Расстояния между городами заданы матрицей (Если между городами i,j есть прямой путь с расстоянием N, то элементы матрицы A(i,j) и A(j,i) содержат значение N, иначе 0). Написать программу поиска минимального пути обхода всех городов без посещения дважды одного и того же города (задача коммивояжера).
25. Задан набор слов. Построить из них любую цепочку таким образом, чтобы символ в конце слова совпадал с символом в начале следующего.
26. Задан массив целых. Построить из них любую последовательность таким образом, чтобы последняя цифра предыдущего числа совпадала с первой цифрой следующего.
27. Для данного n напечатайте коэффициенты разложения полинома (1 + x)n.
28. Вычислить, используя рекурсию, выражение
где матрица Bk получается из A вычеркиванием первой строки и k-го столбца.
22. Написать функцию определения, является ли заданное натуральное число простым.
23. Реализовать рекурсивный алгоритм построения цепочки из имеющегося набора костей домино.
24. Расстояния между городами заданы матрицей (Если между городами i,j есть прямой путь с расстоянием N, то элементы матрицы A(i,j) и A(j,i) содержат значение N, иначе 0). Написать программу поиска минимального пути обхода всех городов без посещения дважды одного и того же города (задача коммивояжера).
25. Задан набор слов. Построить из них любую цепочку таким образом, чтобы символ в конце слова совпадал с символом в начале следующего.
26. Задан массив целых. Построить из них любую последовательность таким образом, чтобы последняя цифра предыдущего числа совпадала с первой цифрой следующего.
27. Для данного n напечатайте коэффициенты разложения полинома (1 + x)n.
28. Вычислить, используя рекурсию, выражение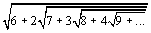 29. Написать процедуру печати всех перестановок из n символов.
30. Написать процедуру перевода числа из десятичной системы счисления в двоичную.
29. Написать процедуру печати всех перестановок из n символов.
30. Написать процедуру перевода числа из десятичной системы счисления в двоичную.
Назад
На главную
Нет комментариев.
Оставить комментарий:
|
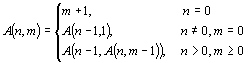
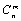 по следующей формуле:
по следующей формуле: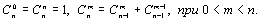
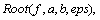 которая методом деления отрезка пополам (методом дихотомии) находит с точностью eps корень уравнения f(x) = 0 на отрезке [a,b] (
которая методом деления отрезка пополам (методом дихотомии) находит с точностью eps корень уравнения f(x) = 0 на отрезке [a,b] (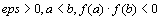 ). Метод дихотомии определяется следующим образом. Если f(a) и f(b) имеют разные знаки, то между точками a и b существует корень R. Пусть
). Метод дихотомии определяется следующим образом. Если f(a) и f(b) имеют разные знаки, то между точками a и b существует корень R. Пусть 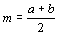 – средняя точка в интервале
– средняя точка в интервале 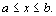 Если f(m) = 0, то корень R=m. Если нет, то либо f(a) и f(m) имеют разные знаки
Если f(m) = 0, то корень R=m. Если нет, то либо f(a) и f(m) имеют разные знаки 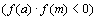 , либо f(m) и f(b) имеют разные знаки
, либо f(m) и f(b) имеют разные знаки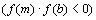 . Если
. Если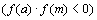 , то корень лежит в интервале
, то корень лежит в интервале 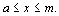 В противном случае он лежит в интервале
В противном случае он лежит в интервале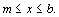 Теперь выполним это действие для нового интервала – половины исходного интервала. Процесс продолжается до тех пор, пока интервал не станет меньше eps.
Теперь выполним это действие для нового интервала – половины исходного интервала. Процесс продолжается до тех пор, пока интервал не станет меньше eps.