| Структура данных и алгоритмы на языке Pascal |
Статистический анализ
Большинство людей, пользующихся ЭВМ, в какой-то мере используют их для статистического анализа. Такой анализ может принимать форму предсказания изменений курса акций, выполнения клинических тестов для определения границ применения нового лекарства или даже определения средних результатов команд из Младшей Лиги. Ветвь математики, которая занимается обобщением, обработкой и экстраполяцией данных, называется статистическим анализом.
Как отдельная дисциплина статистический анализ стал рассматриваться не так давно. Он появился в 70-е годы в результате изучения игр со случайными событиями. Статистический анализ и теория вероятности в действительности сильно связаны друг с другом. Современные подходы к статистическому анализу сложились на рубеже нынешнего столетия, когда стали доступны для обработки большие наборы данных. Применение ЭВМ позволяет быстро находить связь и обрабатывать очень большие наборы данных, а также представлять их в удобной для человека форме. Теперь, когда все больше информации создается и используется правительством и средствами массовой информации, почти каждый аспект жизни подвергается статистической обработке. Практически нельзя слушая радио, смотря телевизор или читая газеты не получить некоторую статистическую информацию.
Хотя Паскаль не разрабатывался специально для программирования задач по статистическому анализу, он достаточно хорошо подходит для этой цели. В некоторых случаях он обладает даже большей гибкостью, чем некоторые языки экономической ориентации, например, Кобол и Бейсик. Одним из преимуществ Паскаля над Коболом является простота использования графического интерфейса для выдачи графиков данных. Кроме того, математические подпрограммы Паскаля работают значительно быстрее, чем большинство таких подпрограмм в других языках.
Рассмотрим расчет следующих величин, используемых в статистическом анализе:
- среднего значения;
- медианы;
- моды;
- стандартного отклонения;
- коэффициента регрессии;
- коэффициента корреляции.
Кроме того, дается несколько простых методов графического вывода.
ВЫБОРКИ, ГЕНЕРАЛЬНЫЕ СОВОКУПНОСТИ, РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ И ПЕРЕМЕННЫЕ
Прежде чем перейти к статистическому анализу, следует познакомиться с некоторыми ключевыми понятиями. Для получения статистических данных сначала берется выборка определенных значений данных, на основании которой затем делаются обобщающие выводы. Каждая выборка берется из генеральной совокупности, представляющей собой все возможные значения, которые могут быть в исследуемой ситуации. Например, если оценивать результаты работы фабрики, выпускающей ящики, по данным выпуска только за каждую среду и делая по ним вывод о выпуске за весь год, то здесь выборка представляет собой данные о выпуске по всем средам года и является частью генеральной совокупности данных о ежедневном выпуске за год.
Выборка может совпадать с генеральной совокупностью и в этом случае она будет исчерпывающей. Для приведенного примера выборка будет совпадать с генеральной совокупностью в том случае, когда будут использоваться данные о выпуске по всем пяти дням в неделю в течение года. Если выборка меньше генеральной совокупности, то всегда результат может иметь ошибку. Однако в большинстве случаев можно определить вероятность этой ошибки. В этой главе предполагается, что выборка совпадает с генеральной совокупностью, и следовательно, такие ошибки не рассматриваются.
При оценке результатов выборов и проведении опросов общественного мнения результаты относительно небольшой выборки распространяются на все население. Например, статистическую информацию о курсе акций Доу Джонса можно использовать для оценки курса акций на всем рынке. Конечно, достоверность таких выводов может меняться в широком диапазоне. В других случаях выборка, совпадающая или почти совпадающая с генеральной совокупностью, используется для суммирования большого набора чисел и упрощения обработки. Например, в отчетах органов образования обычно приводятся средние оценки для класса вместо индивидуальных оценок учащихся.
Статистика зависит от распределения случайных событий в генеральной совокупности. Из нескольких широко распространенных в природе наиболее важным (и единственным рассматриваемым в этой главе) является нормальное распределение. Наиболее вероятными значениями являются средние значения. И действительно, график этого распределения полностью симметричен относительно своей вершины, которая представляет также среднее значение. Чем дальше расстояние от среднего значения, тем меньше вероятность события. Многие ситуации в реальной жизни описываются нормальным распределением.
В любом статистическом процессе имеется независимая переменная, которая является предметом изучения, и зависимая переменная, которая является фактором, влияющим на независимую переменную. В этой главе в качестве зависимой переменной используется время (как промежуток между соседними событиями). Например, исследуя курсы акций, вы можете захотеть рассмотреть их изменения в течение дня. Вам поэтому потребуется изучить изменения курса акций в течение заданного периода без относительно к действительной календарной дате.
В этой главе будут разработаны отдельные статистические функции и затем они будут объединены в одну программу, которая работает с помощью меню. Эта программа может использоваться для разнообразного статистического анализа. Она также может использоваться для вывода графиков на экран.
Элементы выборки в дальнейшем будут обозначаться буквой D с индексом от I до N, где N является номером последнего элемента.
Основные статистические оценки
Статистический анализ во многих случаях основывается на получении трех важных величин, которые имеют также самостоятельное значение. Этими величинами являются среднее значение, медиана и мода.
Среднее значение
Среднее значение или арифметическое среднее наиболее широко используется в статистике. Это одно значение может использоваться для представления некоторого набора данных. В этом случае среднее значение можно назвать "центром тяжести" этого набора. Среднее значение вычисляется следующим образом: складываются все значения выборки и результат делится на общее число значений. Например, сумма набора значений
1 2 3 4 5 6 7 8 9 10
равна 55. Если это значение разделить на число элементов выборки, равное десяти, то получим среднее значение 5,5.
При разработке статистических функций на Паскале будем считать, что все данные хранятся в массиве чисел с плавающей запятой с названием "DataArray", тип которого определяется пользователем. Будем считать, что число элементов выборки известно. Все функции и процедуры будут использовать массив "data" для хранения выборки и переменную "num" для хранения числа элементов. Приводимая ниже функция вычисляет среднее значение для массива из "num" чисел с плавающей запятой. Результат получается в виде данного типа числа с плавающей запятой:
{ вычисление среднего значения }
function mean(data: DataArray; num: integer): real;
var
t: integer;
avg: real;
begin
avg:=0;
for t:= 1 to num do avg:=avg+data[t];
mean:= avg/num;
end; { конец вычисления среднего значения }
Например, если вы вызовете функции "Mean" с десятиэлементным массивом, содержащим числа от 1 до 10, то в результате получите 5,5.
Медианы
Медианой выборки является среднее значение из всего упорядоченного набора значений. Например, для выборки
1 2 3 4 5 6 7 8 9
медианой будет 5, поскольку это число находится в середине. В на боре значений
1 2 3 4 5 6 7 8 9 10
в качестве медианы может использоваться 5 или 6. В хорошо упорядоченной выборке, какой является выборка с нормальным распределением, среднее значение и медиана имеют очень близкие значения. Однако по мере увеличения отклонения закона распределения выборки от нормального увеличивается разница между медианой и средним значением. Медиана вычисляется путем сортировки выборки в порядке возрастания значений и выбора среднего значения с индексом N/ 2.
Результатом приводимой ниже функции "Median" является значение среднего элемента выборки. Для сортировки массива данных используется модифицированная версия процедуры быстрой сортировки:
{ версия процедуры быстрой сортировки для упорядочения целых чисел }
procedure QuickSort(var item: DataArray; count: integer);
procedure qs(l, r: integer; var it: DataArray);
var
i, j: integer;
x, y: DataItem;
begin
i: = l; j: = r;
x: = it[(l+r) div 2];
repeat
while it[i] < x do i:= i+1;
while x < it[j] do j:= j-1;
if i<=j then
begin
y:= it[i];
it[i]:= it[j];
it[j]:= y;
i: = i+1; j:= j-1;
end;
until i>j;
if l<j then qs(l, j, it);
if l<r then qs(i, r, it)
end;
begin
qs(1, count, item);
end; {QuickSorte}
{ поиск медианы }
function median(data: DataArray; num: integer): real;
var
dtemp: DataArray;
t: integer;
begin
for t:=1 to num do dtemp[t]:=data[t];
QuickSort(dtemp, num);
median: = dtemp[num div 2];
end;
Мода
Модой выборки называется значение, которое встречается большее число раз в выборке. Например, в наборе значений
1 2 3 4 5 6 7 8 9 3 6 6
модой является число 6, поскольку оно встречается три раза. Мода может иметь несколько значений. Например, в выборке значений
10 20 30 40 50 60 70
имеется две моды (30 и 60), поскольку каждая из них встречается по два раза.
Результатом функции "FindMode" является мода выборки. Если имеется несколько значений моды, то в результате будет получено последнее значение.
{ поиск моды }
function FindMode(data: DataArray; num: integer); real;
var
t, w, count, oldcount: integer;
md, oldmd: real;
begin
oldmd := 0; oldcount := 0;
for t := 1 to num do
begin
md := data[t];
count := 1;
for w := t+1 to num do
if md=data[w] then count := count+1;
if count>oldcount then
begin
oldmd := md;
oldcount := count;
end;
end;
FindMode := oldmd;
end; { конец процедуры поиска моды }
Применение среднего значения, медианы и моды
Среднее значение, медиана и мода служат одной цели, а именно, обеспечению одного значения, обобщающего все значения выборки. Однако, каждое из них представляет выборку по разному. Обычно чаще всего используется среднее значение выборки. Поскольку при вычислении среднего значения делается суммирование всех значений выборки, оно является действительно отражением всех элементов выборки. Основным недостатком среднего значения является чувствительность к одному экстремальному значению. Например, пусть в некой фирме "Уидгет" заработок владельца составляет 100000 долларов в год, а заработок каждого из девяти рабочих составляет 10 000 долларов в год. Средний заработок в этой фирме будет равен 19 000 долларов в год, однако, эта цифра недостаточно правильно описывает ситуацию в фирме.
В случаях, аналогичных описанному, иногда вместо среднего значения используется мода. Мода заработков в фирме "Уидгет" равна 10 000 долларов в год и эта цифра более правильно отражает реальную ситуацию в фирме. Однако мода также может вводить в заблуждение. Пусть некоторая автомобильная фирма производит автомобили пяти различных цветов. За некоторую неделю было получено:
- 100 зеленых автомобилей;
- 100 оранжевых автомобилей;
- 150 синих автомобилей;
- 200 черных автомобилей;
- 190 белых автомобилей.
Здесь модой выборки являются черные автомобили, поскольку было произведено 200 черных автомобилей, что превышает число автомобилей любого другого цвета. Однако неправильно делать вывод о том, что автомобильная фирма производит в основном автомобили черного цвета.
Медиана представляет интерес для тех случаев, когда оправдано предположение о нормальном распределении. Например, если выборка представляет собой следующий набор:
1 2 3 4 5 6 7 8 9 10
то медианой будет 5 или 6, а среднее значение 5,5. В этом случае медиана близка к среднему значению. Однако, в следующей выборке
1 1 1 1 5 100 100 100 100
медиана по-прежнему равна 5, а среднее значение приблизительно равно 46.
В определенных случаях ни среднее значение, ни медиана, ни мода не могут дать достоверную картину. Это приводит к использованию двух наиболее важных статистических величин - дисперсии и стандартного отклонения.
Дисперсия и стандартное отклонение
Хотя для оценки всей выборки очень удобно использовать лишь одно значение /такое как среднее значение, мода или медиана/, этот подход легко может привести к неправильным выводам. Нетрудно понять, что причина такого положения лежит не в самой величине, а в том, что одна величина никак не отражает разброс значений данных. Например, в выборке
1 1 1 1 9 9 9 9
среднее значение равно 5. Однако в самой выборке нет ни одного элемента со значением 5. Возможно, вам потребуется знать степень близости каждого элемента выборки к ее среднему значению. Или, другими словами, вам потребуется знать дисперсию значений. Зная степень изменения данных вы можете лучше интерпретировать среднее значение, медиану и моду. Степень изменения значений выборки определяется путем вычисления их дисперсии и стандартного отклонения.
Дисперсия и квадратный корень из дисперсии, называемый стандартным отклонением, характеризуют среднее отклонение от среднего значения выборки. Среди этих двух величин наиболее важное значение имеет стандартное отклонение. Это значение можно представить как среднее расстояние, на котором находятся элементы от среднего элемента выборки.
Дисперсию трудно интерпретировать содержательно. Однако, квадратный корень из этого значения является стандартным отклонением и хорошо поддается интерпретации. Стандартное отклонение вычисляется путем определения сначала дисперсии и затем вычисления квадратного корня из дисперсии.
Например, для выборки
11 20 40 30 99 30 50
будут получены следующие значения:
D D-M (D-M)
11 -29 841
20 -20 400
40 0 0
30 -10 100
99 59 3491
30 -10 100
50 10 100
Сумма 280 0 5022
Среднее
значение 40 0 717,42
Здесь среднее значение квадратов разностей равно 717,42. Для получения стандартного отклонения осталось лишь взять квадратный корень из этого числа. Результат составит приблизительно 26,78. Следует помнить, что стандартное отклонение интерпретируется как среднее расстояние, на котором находятся элементы от среднего значения выборки.
Стандартное отклонение показывает, насколько хорошо среднее значение описывает всю выборку. Если вы являетесь владельцем конфетной фабрики и в полученном отчете говорится, что дневной выпуск за последний месяц составил 2500 упаковок, но при стандартном отклонении в 2000, то вы будете знать, что производственная линия требует лучшего управления.
Если ваша выборка подчиняется стандартному нормальному закону распределения, то около 68% значений выборки будут находиться в рамках одного стандартного отклонения от среднего значения и около 95% будут находиться в рамках двух стандартных отклонений.
Ниже приводится функция, которая вычисляет стандартное отклонение для заданной выборки:
{ вычислить стандартное отклонение }
function StdDev(data: DataArray; num: integer):real;
var
t: integer;
std, avg: real;
begin
avg:= mean(data, num);
std := 0;
for t := 1 to num do
std := std+(data[t]-avg)*(data[t]-avg));
std := std/num;
StdDev := sqrt(std);
end; { конец функции вычисления стандартного отклонения }
Вывод на экран простых графиков
Применение графиков в статистике позволяет просто и точно передать смысл данных. График позволяет сразу же понять, как распределены данные и как изменяются их значения. Здесь рассматриваются только двумерные графики, использующие двумерную систему координат X-Y. /Получение трехмерных графиков является отдельной дисциплиной и выходит за рамки данной книги/.
Имеется две распространенные формы двумерных графиков: столбиковые диаграммы и точечные графики. В столбиковой диаграмме каждое значение представляется заштрихованным столбиком. На точечном графике каждый элемент изображается точкой с координатами X и Y. Примеры графиков показаны на рис.1.
 |
Рис.1. Примеры столбиковой диаграммы (а) и точечного графика (б)
Столбиковая диаграмма обычно используется при относительно небольшом количестве данных, например, при представлении валового национального продукта за последние десять лет или ежемесячного выпуска на предприятии в процентном отношении. Точечные графики обычно используются при выводе большого числа данных, например, для вывода ежедневного курса акций некоторой фирмы в течение года. Применение получила также модификация точечного графика, когда соседние точки соединяют линией.
Разработанные в этой главе графические функции требуют применения ПЭВМ фирмы IBM (или совместимых с ними ПЭВМ) с графическим адаптером CGA или EGA. Эти подпрограммы рассчитаны на применении четвертого режима вывода графиков. Графические подпрограммы используют графические функции Паскаля версии 4, которые отличаются от графических функций предыдущих версий. Если вы используете предыдущую версию Паскаля, то вам потребуется сделать соответствующие изменения.
Используются следующие графические функции:
Название Назначение
---------------- ----------------------------------------------
InitGraph Инициирует графическое оборудование
SetColor Устанавливает цвет рисунка для большинства
графических программ
SetLine Определяет тип линий, выводимых посредством
процедуры "Line"
Line Выводит линии на экран с текущим цветом
PupPixel Выводит элемент изображения в заданном цвете
RestoreCrtMode Восстанавливает режим работы видеотерминала
в состояние до вызова "InitGraph"
OutTextXY Записывает строку в заданную позицию,
находясь в графическом режиме работы
Эти подпрограммы используют блок "Graph". Подробное описание этих и других графических функций дается в справочном руководстве по языку Паскаль версии 4.
Ниже приводится простая графическая функция, формирующая столбиковую диаграмму на ПЭВМ фирмы IBM:
uses
crt, graph;
const
MAX = 100;
type
DataItem = real;
DataArray = array [1..MAX] of DataItem;
var
data: DataArray;
procedure Simpleplot(data: DataArray; num: integer);
var
t, incr:integer;
a: real;
ch: char;
GraphDriver, Craphmode : ineger;
x, y : integer;
begin
{ установка режима 4 для адаптеров EGA и CGA }
GraphDriver := CGA ;
Craphmode := CGAC1 ;
InitGraph(GraphDriver, Craphmode, '');
SetColor(1);
SetLineStyle(Solid, 0, NormWidth);
{ вычерчивание сетки }
OutTextXY(0, 191, '0'); { минимум }
OutTextXY(0, 0, '190'); { максимум }
OutTextXY(290, 191, '300'); { число }
for t := 1 to 19 do PutPixel(0, t*10, 1);
SetColor(3);
Line(x, 190, x, 190-y);
SetColor(2);
for t := 1 to num do
begin
a := data[t];
y := trunc(a);
incr := 10;
x := ((t-1)*incr)+20
Line(x, 190, x, 190-y);
end;
ch:= ReadKey;
RestoreCrtMode;
end; { конец процедуры вывода простого графика }
Для ПЭВМ фирмы IBM режим с максимальной разрешающей способностью в 320х200 точек устанавливается с помощью процедуры "InitGraph". Процедура "OutTextXy" устанавливает курсор в позицию с требуемыми координатами Х и Y и делает вывод заданной строки. Процедура "Line" имеет следующую общую форму: Line (начало_Х, начало_Y, конец_Х, конец_Y), где все значения задаются целыми числами. При выводе строки используется текущий цвет, определенный при вызове процедуры "SetColor".
В этом примере процедура вывода графика обладает серьезным недостатком. Предполагается, что все данные находятся в диапазоне от нуля до 190, поскольку только эти значения можно задавать при вызове графической функции "Line". Это предположение хорошо сработает в маловероятном случае, когда ваши данные точно будут лежать в этом диапазоне. Для вывода данных в любом диапазоне значений эти данные должны быть нормализованы перед выводом так, чтобы не выходить за допустимый диапазон значений. Нормализация заключается в поиске коэффициента отношения действительного диапазона значений данных и физического диапазона разрешающей способности экрана. Значение каждого данного затем должно быть умножено на этот коэффициент и получено число, попадающее в диапазон экрана. Нормализация по оси Y должна делаться по следующей формуле:
250
Y = Y * --------- ,
(max-min)
где Y является тем значением, которое передается процедуре вывода графика. Та же формула должна использоваться для расширения шкалы, когда диапазон значений данных очень маленький. В таком случае экран дисплея будет использоваться наиболее рационально.
Функция "BarPlot" масштабирует оси Х и Y и выводит столбиковый график для 300 элементов. Предполагается, что по оси Х задается время с единичным шагом. Процедура нормализации находит минимальное и максимальное значение в выборке и затем вычисляет их разницу. Это число, которое представляет разброс между минимальным и максимальным значениями, затем делится на разрешающую способность экрана. Для графического режима 4 это число равно 190 для оси Y и 300 для оси Х /поскольку требуется место для граничных полей и основной строки/. Полученный коэффициент затем используется для масштабирования данных выборки.
{ вывод столбиковой диаграммы }
procedure BarPlot(data: DataArray; num: integer);
var
x, y, max, min, incr, t:integer;
a, norm, spread: real;
ch: char;
value: string[80];
begin
{ установка режима 4 для адаптеров EGA и CGA }
GraphDriver := CGA ;
Craphmode := CGAC1 ;
InitGraph(GraphDriver, Craphmode, '');
SetColor(1);
SetLineStyle(Solid, 0, NormWidth);
{ сначала для нормализации находится минимальное и максимальное значение }
max := getmax(data, num)
min := getmin(data, num)
if min>0 then min := 0;
spread := max - min;
norm := 190/spread;
{ вычерчивание сетки }
str(min, value);
OutTextXY(0, 191, value); { минимум }
str(max, value);
OutTextXY(0, 0, value); { максимум }
str(num, value);
OutTextXY(300, 191, value); { число }
for t := 1 to 19 do PupPixel(0, t*10, 1);
SetColor(3);
Line(0, 190, 320, 190);
SetColor(2);
{ вывод данных }
for t := 1 to num do
begin
a := data[t]-min;
a := a*norm;
y := trunc(a);
incr := 300 div num;
x := ((t-1)*incr)+20
Line(x, 190, x, 190-y);
end;
ch := Readkey;
RestoreCrtMode;
end; { BarPlot }
Эта версия программы, кроме того, делает вывод точек по оси Y. Расстояние между точками равно 1/20 разнице между максимальным и минимальным значением. На рис.2 приводится пример столбиковой диаграммы для двадцати элементов, полученной с помощью процедуры "BarPlot". Конечно, эта процедура не обладает всеми желательными свойствами, но она дает хороший вывод одной выборки. Эту процедуру можно легко усовершенствовать и сделать ее более удобной для конкретного случая.
 |
Рис 2. Пример столбиковой диаграммы, полученной с помощью процедуры "BarPlot"
Для получения процедуры по выводу точечных графиков требуется сделать только небольшие изменения в процедуре "BarPlot". Основное изменение связано с заменой функции "Line" на функцию вывода одной точки. Для этого используется функция "PutPixel". В общем, виде она записывается в следующей форме: PutPixel(x,y,цвет) где все аргументы являются целыми числами. Цвет каждой выводимой точки задается параметром "цвет". Для режима 4 он должен принимать значения от 0 до 3. Ниже приводится функция "ScatterPlot":
{ вывод точечного графика }
procedure ScatterPlot(data: DataArray; num, ymin, ymax, xmax, xmin: integer);
var
x, y, incr, t:integer;
a, norm, spread: real;
ch: char;
value: string[80];
begin
{ сначала для нормализации находится минимальное и максимальное значение }
if ymin>0 then ymin := 0;
spread := ymax - ymin;
norm := 190/spread;
{ вычерчивание сетки }
str(ymin, value);
OutTextXY(0, 191, value); { минимум }
str(ymax, value);
OutTextXY(0, 0, value); { максимум }
str(xmax, value);
OutTextXY(300, 191, value); { число }
SetColor(3);
for t := 1 to 19 do PutPixel(0, t*10, 1);
Line(0, 190, 320, 190);
SetColor(2);
{ вывод данных }
for t := 1 to num do
begin
a := data[t]-ymin;
a := a*norm;
y := trunc(s);
incr := 300 div xmax;
x := ((t-1)*incr)+20;
PutPixel(x, 190-y, 2);
end;
end; { конец процедуры вывода точечного графика}
В процедуре "BarPlot" минимальное и максимальное значение вычисляется внутри процедуры. В отличие от этой процедуры в процедуре "ScatterPlon" не делается этих вычислений, а минимальное и максимальное значения передаются самой процедуре. Это позволяет выводить сразу несколько графиков на один экран без изменения масштаба, накладывая, таким образом, один график на другой.
Прогнозирование и уравнение регрессии
Статистическая информация часто используется для вывода "обоснованных предположений" о будущем. Хотя каждому известно, что на основе прошлого опыта не обязательно можно предсказать будущее и что каждое правило имеет исключение, все же данные о прошлом используются для этого. Очень часто тенденции, имевшие место в прошлом и настоящем, сохраняются и в будущем. В этих случаях вы можете определить конкретные значения для некоторого времени в будущем. Этот процесс называется прогнозированием или анализом тенденций.
Например, рассмотрим некое исследование продолжительности жизни за десятилетний период. Пусть получены следующие данные:
Год Продолжительность жизни
1980 69
1981 70
1982 72
1983 68
1984 73
1985 71
1986 75
1987 74
1988 78
1989 77
Сначала следует понять, если здесь какая-нибудь тенденция? Если она действительно имеется, то можно узнать какой она имеет характер. И, наконец, если наблюдается действительно заметная тенденция, то можно предсказать, например, среднюю продолжительность в 1995 году. Сначала рассмотрим столбиковую диаграмму и точечный график для этих данных, представленные на рис.3. Исследуя их, можно сделать вывод, что средняя продолжительность жизни в целом увеличивается. Если приложить линейку так, чтобы наилучшим образом линия соответствовала графику, и продолжить линию до 1995 года, то окажется, что продолжительность жизни будет в районе 82. Однако, насколько можно быть уверенным в достоверности такого вывода?
Несмотря на интуитивное ощущение правильности такого вывода вы можете захотеть использовать более формальные и точные методы по прогнозированию тенденции средней продолжительности жизни. Имея набор изменяющихся во времени данных лучше всего получать прогноз путем поиска линии наилучшего соответствия по отношению к имеющимся данным. Именно это делалось с применением линейки. Линия наилучшего соответствия располагается наиболее близко ко всем точкам и лучше всего отражает их тенденцию. Хотя некоторые или даже все данные не будут находиться на линии, сама линия хорошо представляет их. Достоверность линии зависит от близости точек выборки. Линия в двумерном пространстве задается следующим основным уравнением:
Y = a + bX,
где Y является независимой переменной, Х является зависимой переменной, "а" является точкой пересечения оси Y, а "в" задает наклон линии. Таким образом, для определения линии наилучшего соответствия выборки требуется определить "а" и "в".
 |
Рис.3. Столбиковая диаграмма, /а/ для прогноза средней продолжительности жизни
Для определения значений этих параметров можно использовать несколько методов, но наиболее распространенным (и, как правило, наилучшим) является метод наименьших квадратов. Этот метод построен на минимизации расстояния от действительных значений данных до линии. Этот метод состоит из двух шагов: сначала вычисляется "в" (наклон линии) и затем вычисляется "а" (пересечение оси Y).
Вывод этой формулы выходит за рамки этой книги. Получив "в" вы можете, используя этот параметр, вычислить "а": Определив значения параметров "а" и "в" вы можете, задав любое значение Х, найти соответствующее значение Y. Например, используя приведенные выше данные по средней продолжительности жизни, можно получить следующее уравнение регрессии:
Y = 67,46 + 0,95 * X.
Следовательно, для нахождения ожидаемой продолжительности жизни в 1995 году (15 лет от 1980 года) делаются следующие вычисления:
67,46 + 0,95*15 = 82.
Однако, даже имея для данных линию наилучшего соответствия вам может потребоваться знание действительной корреляции данных с этой линии. Если линия и данные слабо коррелированны, то будет мало пользы от линии регрессии. Однако, если линия хорошо соответствует данным, то по ней можно делать очень достоверный прогноз. Наиболее распространенным способом определения и представления корреляции данных и линии регрессии является вычисление коэффициентов корреляции, которые могут принимать значения от нуля до единицы. Коэффициенты корреляции по существу определяет степень близости каждой точки к линии. Если коэффициент корреляции имеет единичное значение, то данные хорошо соответствуют линии /т.е. каждый элемент выборки также находится на линии регрессии/. Если коэффициент корреляции имеет нулевое значение, то никакое значение из выборки не располагается на линии. В действительности коэффициент корреляции может принимать любое значение из диапазона от нуля до единицы. Коэффициент корреляции вычисляется по формуле, приведенной на следующей странице.
Здесь М является средним значением координаты Х и М является средним значением координаты Y. Обычно в качестве сильной корреляции рассматривается значение 0,81. В этом случае 66% данных соответствует линии регрессии. Для получения процентного соотношения необходимо просто возвести в квадрат значение коэффициента корреляции. Ниже приводится функция "Regress". В ней используется описанный выше метод поиска коэффициентов регрессии и коэффициентов корреляции:
{ вычисление коэффициентов регрессии и вывод линии регрессии}
procedure Regress(data: DataArray; num: integer);
var
a, b, x_avg, y_avg, temp, temp2, cor: real;
data2: DataArray
t, min, max: integer;
ch: char;
begin
{ поиск среднего значения Х и У }
y_avg := 0; x_avg := 0;
for t := 1 to num do
begin
y_avg := y_avg + data[t];
x_avg := x_avg + t; { поскольку Х представляет собой время }
end;
x_avg := x_avg/num;
y_avg := y_avg/num;
{ поиск коэффициента 'в' уравнения регрессии }
temp := 0; temp2 := 0;
for t := 1 to num do
begin
temp := temp +(data[t] - y_avg)*(t-x_avg);
temp2 := temp2 +(t - x_avg)*(t-x_avg);
end;
b := temp/temp2;
{ поиск коэффициента 'a' уравнения регрессии }
a := y_avg-(b*x_avg);
{ вычисление коэффициента корреляции }
for t := 1 to num do data2[t] := t;
cor := temp/num;
cor := cor/(StdDev(data, num)*StdDev(data2,num);
Writeln('Уравнение регресии : Y = ', a: 15: 5, '+',b: 15: 5, '* X');
Writeln('Коэффициент корреляции : ', cor: 15:5);
Writeln('Вывести данные и линию регрессии ? (y/n)');
Readln(ch);
ch := upcase(ch);
if ch <> 'N' then
begin
{ установка режима 4 для адаптеров EGA и CGA }
GraphDriver := CGA ;
Craphmode := CGAC1 ;
InitGraph(GraphDriver, Craphmode, '');
SetColor(1);
SetLineStyle(Solid, 0, NormWidth);
{ вывод графиков }
for t := 1 to num*2 do data2[t] := a+(b*t);
{ массив регрессии }
min:= getmin(data, num)*2;
max:= getmax(data, num)*2;
ScatterPlot(data, num, min, max. num*2);
ScatterPlot(data2, num*2, min, max, num*2);
ch := ReadKey;
RestoreCrtMode;
end;
end; { конец процедуры вычисления коэффициентов регрессии и корреляции }
При проведении прогнозирования подобно описанному выше следует помнить, что по данным о прошлом не всегда можно предсказать будущее. Однако в тех случаях, когда это можно сделать, могут получить очень интересные результаты.
ПОЛНАЯ ПРОГРАММА ПО СТАТИСТИЧЕСКОМУ АНАЛИЗУ
К этому моменту в этой главе были разработаны несколько функций по выполнению статистических вычислений для генеральных совокупностей с одной переменной. В этом разделе эти функции будут собраны в одну программу по анализу данных, выводу стол - битовых диаграмм, точечных графиков и прогнозирования. Перед проектированием такой программы необходимо определить запись для хранения переменных данных и несколько необходимых вспомогательных подпрограмм.
Прежде всего, нам потребуется массив для хранения значений выборки. Можно использовать одномерный массив чисел с плавающей точкой 'data' с размером МАХ. Максимальное значение должно выбираться таким, чтобы вместить максимальную выборку. В нашем случае это число равно 100. Ниже дается определение констант и типов, а также глобальных переменных:
Uses Crt, Graph; const MAX = 100; type str80 = string[80]; DataItem = real; DataArray = array [1..80] of DataItem; var data: DataArray; a, m, md, std: real; num: integer; ch: char; datafile: file of DataItem; GraphDriver, Craphmode : ineger;
Кроме уже разработанных статистических функций вам потребуется также подпрограммы по сохранению и загрузке данных. Подпрограмма "Save" должна также сохранить число элементов данных, а подпрограмма "Load" должна считывать это число.
{ сохранить данные }
procedure Save(data: DataArrary; num: integer):
var
t: integer;
fname: string[80];
temp: real;
begin
Write('Enter Filename: ');
Readln(fname);
Assign(datafile,fname);
rewrite(datafile);
temp := num;
write(datafile,temp);
for t := 1 to num do write(datafile,data[t]);
close(datafile);
end;
{ загрузить данные }
procedure Load;
var
t: integer;
fname: string[80];
temp: real;
begin
Write('Enter Filename: ');
Readln(fname);
Assign(datafile,fname);
reset(datafile);
Read(datafile,temp);
num := trunc(temp);
for t := 1 to num do Read(datafile,data[t]);
close(datafile);
end;
Ниже приводится полная программа по статистическому анализу:
program stats;
Uses
Crt, Graph;
const
MAX = 100;
type
str80 = string[80];
DataItem = real;
DataArray = array [1..80] of DataItem;
var
data: DataArray;
a, m, md, std: real;
num: integer;
ch: char;
datafile: file of DataItem;
GraphDriver, Craphmode : integer;
{ версия быстрой сортировки для целых чисел }
procedure QuickSort(var item: DataArray; count: integer);
procedure qs(l, r:integer; var it: DataArray);
var
i, j: integer;
x, y: DataItem;
begin
i := l; j := r;
x := it[(l+r) div 2];
repeat
while it[i] < x do i := i+1;
while x < it[j] do j := j-1;
if i <= j then
begin
y := it[i];
it[i] := it[j];
it[j] := y;
i := i+1; j := j-1;
end;
until i>j;
if l<j then qs(l, j, it);
if l<r then qs(i, r, it );
end;
begin
qs(1, count, item)
end; { QuickSort }
{ эта функция возвращает значение "истина", если в строке "s" находится символ "сh" }
function is_in(ch: char; s: str80): boolean;
var
t: integer;
begin
is_in := FALSE;
for t:=1 to length(s) do
if s[t]=ch then is_in := TRUE;
end; { is_in }
{ возвращает код функции, выбранной пользователем из меню }
function menu:char;
var
ch: char;
begin
Writeln;
repeat
Writeln('Enter data');
Writeln('Display data');
Writeln('Basic statistics');
Writeln('Regression line and scatter plot');
Writeln('Plot a bar graph');
Writeln('Save');
Writeln('Load');
Writeln('Quit');
Writeln;
Write('choose one (E, D, B, R, P, S, L, Q): ');
Readln(ch);
ch := upcase(ch);
until is_in(ch,'EDBRPSLQ');
menu := ch;
end; { menu }
{ вывод текущего набора данных }
procedure Display(data: DataArray; num: integer);
var
t: integer;
begin
for t := 1 to num do Writeln(t, ': ',data[t]);
Writeln;
end; { Display }
{ ввод данных пользователя }
procedure Enter(var data: DataArray);
var
t: integer;
begin
Writeln('number of items?: ');
Readln(num);
for t := 1 to num do begin
Writeln('enter item ',t, ': ');
Readln(data[t]);
end;
end; { enter }
{ вычисление среднего значения }
function mean(data: DataArray; num: integer): real;
var
t: integer;
avg: real;
begin
avg := 0;
for t := 1 to num do avg := avg+data[t];
mean := avg/num;
end; { mean }
{ вычисление стандартного отклонения }
function StdDev(data: DataArray; num: integer): real;
var
t: integer;
std, avg: real;
begin
avg := mean(data,num);
std := 0;
for t := 1 to num do
std := std +((data[t]-avg)*(data[t]-avg));
std := std/num;
StdDev := sqrt(std);
end; { StdDev }
{ поиск моды }
function FindMode(data: DataArray; num: integer): real;
var
t, w, count, oldcount: integer;
md, oldmd: real;
begin
oldmd := 0; oldcount := 0;
for t := 1 to num do
begin
md := data[t];
count := 1;
for w := t+1 to num do
if md=data[w] then count := count +1;
if count > oldcount then
begin
oldmd := md;
oldcount := count;
end;
end;
FindMode := oldmd;
end; { FindMode }
{ поиск медианы }
function median(data: DataArray; num: integer): real;
var
dtemp: DataArray;
t: integer;
begin
for t := 1 to num do dtemp[t] := data[t];
QuickSort(dtemp,num);
median := dtemp[num div 2];
end; { median }
{ поиск максимального значения данных }
function getmax(data: DataArray; num: integer):integer;
var
t: integer;
max: real;
begin
max := data[1];
for t := 2 to num do
if data[t]>max then max := data[t];
getmax := trunc(max);
end; { getmax }
{ поиск минимального значения данных }
function getmin(data: DataArray; num: integer):integer;
var
t: integer;
min: real;
begin
min := data[1];
for t := 2 to num do
if data[t]<min then min := data[t];
getmin := trunc(min);
end; { getmin }
{ вывод столбиковой диаграммы }
procedure BarPlot(data: DataArray; num: integer);
var
x, y, max, min, incr, t:integer;
a, norm, spread: real;
ch: char;
value: string[80];
begin
{ установка режима 4 для адаптеров EGA и CGA }
GraphDriver := CGA ;
Craphmode := CGAC1 ;
InitGraph(GraphDriver, Craphmode, '');
SetColor(1);
SetLineStyle(Solidln, 0, NormWidth);
{ сначала для нормализации находится минимальное и максимальное значение }
max := getmax(data, num);
min := getmin(data, num);
if min>0 then min := 0;
spread := max - min;
norm := 190/spread;
{ вычерчивание сетки }
str(min, value);
OutTextXY(0, 191, value); { минимум }
str(max, value);
OutTextXY(0, 0, value); { максимум }
str(num, value);
OutTextXY(300, 191, value); { число }
for t := 1 to 19 do PutPixel(0, t*10, 1);
SetColor(3);
Line(0, 190, 320, 190);
SetColor(2);
{ вывод данных }
for t := 1 to num do
begin
a := data[t]-min;
a := a*norm;
y := trunc(a);
incr := 300 div num;
x := ((t-1)*incr)+20;
Line(x, 190, x, 190-y);
end;
ch := Readkey;
RestoreCrtMode;
end; { BarPlot }
{ вывод точечного графика }
procedure ScatterPlot(data: DataArray; num, ymin, ymax, xmax: integer);
var
x, y, incr, t:integer;
a, norm, spread: real;
ch: char;
value: string[80];
begin
{ сначала для нормализации находится минимальное и максимальное значение }
if ymin>0 then ymin := 0;
spread := ymax - ymin;
norm := 190/spread;
{ вычерчивание сетки }
str(ymin, value);
OutTextXY(0, 191, value); { минимум }
str(ymax, value);
OutTextXY(0, 0, value); { максимум }
str(xmax, value);
OutTextXY(300, 191, value); { число }
SetColor(3);
for t := 1 to 19 do PutPixel(0, t*10, 1);
Line(0, 190, 320, 190);
SetColor(2);
{ вывод данных }
for t := 1 to num do
begin
a := data[t]-ymin;
a := a*norm;
y := trunc(a);
incr := 300 div xmax;
x := ((t-1)*incr)+20;
Putpixel(x, 190-y, 2);
end;
end; { ScatterPlot }
procedure Regress(data: DataArray; num: integer);
var
a, b, x_avg, y_avg, temp, temp2, cor: real;
data2: DataArray;
t, min, max: integer;
ch: char;
begin
{ поиск среднего значения Х и У }
y_avg := 0; x_avg := 0;
for t := 1 to num do
begin
y_avg := y_avg + data[t];
x_avg := x_avg + t; { поскольку Х представляет собой время }
end;
x_avg := x_avg/num;
y_avg := y_avg/num;
{ поиск коэффициента 'в' уравнения регрессии }
temp := 0; temp2 := 0;
for t := 1 to num do
begin
temp := temp +(data[t] - y_avg)*(t-x_avg);
temp2 := temp2 +(t - x_avg)*(t-x_avg);
end;
b := temp/temp2;
{ поиск коэффициента 'a' уравнения регрессии }
a := y_avg-(b*x_avg);
{ вычисление коэффициента корреляции }
for t := 1 to num do data2[t] := t;
cor := temp/num;
cor := cor/(StdDev(data, num)*StdDev(data2,num));
Writeln('Уравнение регрессии : Y = ', a: 15: 5, '+',b: 15: 5, '* X');
Writeln('Коэффициент корреляции : ', cor: 15:5);
Writeln('Вывести данные и линию регрессии ? (y/n)');
Readln(ch);
ch :=upcase(ch);
if ch <> 'N' then
begin
{ установка режима 4 для адаптеров EGA и CGA }
GraphDriver := CGA ;
Craphmode := CGAC1 ;
InitGraph(GraphDriver, Craphmode, '');
SetColor(1);
SetLineStyle(Solidln, 0, NormWidth);
{ получение графиков }
for t := 1 to num*2 do data2[t] := a+(b*t);
min := getmin(data, num)*2;
max := getmax(data, num)*2;
ScatterPlot(data, num, min,max, num*2);
ScatterPlot(data2, num*2, min,max, num*2);
ch := Readkey;
RestoreCrtMode;
end;
end; { regress }
{ сохранить данные }
procedure Save(data: DataArray; num: integer);
var
t: integer;
fname: string[80];
temp: real;
begin
Write('Enter Filename: ');
Readln(fname);
Assign(datafile,fname);
rewrite(datafile);
temp := num;
write(datafile,temp);
for t := 1 to num do write(datafile,data[t]);
close(datafile);
end;
{ загрузить данные }
procedure Load;
var
t: integer;
fname: string[80];
temp: real;
begin
Write('Enter Filename: ');
Readln(fname);
Assign(datafile,fname);
reset(datafile);
Read(datafile,temp);
num := trunc(temp);
for t := 1 to num do Read(datafile,data[t]);
close(datafile);
end; { Load }
begin
repeat
ch := upcase(menu);
case ch of
'E': Enter(data);
'B': begin
a := mean(data, num);
m := median(data, num);
std := StdDev(data,num);
md := FindMode(data,num);
Writeln('mean: ',a: 15: 5);
Writeln('median: ',m: 15: 5);
Writeln('standart deviation: ',std: 15: 5);
Writeln('mode: ',md: 15: 5);
Writeln;
end;
'D': Display(data,num);
'P': BarPlot(data,num);
'R': Regress(data,num);
'S': Save(data,num);
'L': Load;
end;
until ch='Q'
end.
Применение программы статистического анализа
Для того, чтобы показать, как можно пользоваться разработанной в этой главе программой по статистическому анализу, проведем простой анализ акций фирмы "Уидгет". Как вкладчик вы пытаетесь определить целесообразность вклада в данный момент капитала в дело фирмы "Уидгет" посредством покупки ее акций или продажи акций без надежд на быстрое снижение курса с возможностью их покупки по более низкой цене или вклад в другое предприятие. Ниже приводится курс акций фирмы "Уидгет" за последние 24 месяца:
Месяц Курс акций /в долларах/
1 10
2 10
3 11
4 9
5 8
6 8
7 9
8 10
9 10
10 13
11 11
12 11
13 11
14 11
15 12
16 13
17 14
18 16
19 17
20 15
21 15
22 16
23 14
24 18
Сначала следует определить задают ли эти данные какую-нибудь тенденцию. Основные статистические оценки будут следующими:
- среднее значение: 12.08;
- медиана: 11;
- стандартное отклонение: 2.68;
- мода: 11.
Затем получим столбиковую диаграмму для курса акций (рис.4). График говорит о наличии тенденции, однако следует провести регрессионный анализ. Уравнение регрессии будет следующим:
Y = 7.90 + 0.33*X
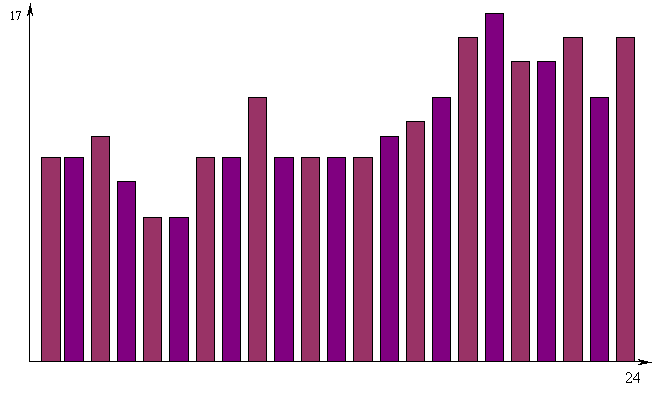 |
Рис. 4. График курса акций фирмы "Уидгет" за последние 24 месяца.
Коэффициент корреляции будет равен 0,85, что соответствует 74%. Это значение является достаточно хорошим, свидетельствующим о наличии заметной тенденции. Очевиден рост курса акций. Такой результат заставит вкладчика отбросить подозрения и приобрести как можно скорее 1000 акций.