| Структура данных и алгоритмы на языке Pascal |
Очереди, стеки, связанные списки и деревья
Программы состоят из алгоритмов и структур данных. Хорошие программы используют преимущества их обоих. Выбор и разработка структуры данных столь же важна, как и разработка процедуры, которая манипулирует ими. Организация информации и методы доступа к ней обычно определяются характером стоящей перед программистом задачи. Поэтому каждый программист должен иметь в своем "багаже" соответствующие методы представления и поиска данных, которые можно применить в каждой конкретной ситуации.
В действительности структуры данных в ЭВМ строятся на основе базовых типов данных, таких как "char", "integer", "real". На следующем уровне находятся массивы, представляющие собой наборы базовых типов данных. Затем идут записи, представляющие собой группы типов данных, доступ к которым осуществляется по одному из данных, а на последнем уровне, когда уже не рассматриваются физические аспекты представления данных, внимание обращается на порядок, в котором данные хранятся и в котором делается их поиск. По существу физические данные связаны с "машиной данных", которая управляет способом доступа к информации в вашей программе. Имеется четыре такие "машины":
- очередь;
- стек;
- связанный список;
- двоичное дерево.
Каждый метод используется при решении определенного класса задач. Каждый метод по существу является неким "устройством", которое обеспечивает для заданной информации определенный способ хранения и при запросе выполняет определенные операции поиска данных. В каждом из этих методов используется две операции: добавить элемент и найти элемент /под элементом понимается некоторая информационная единица/.
ОЧЕРЕДИ
Очередь представляет собой линейный список данных, доступ к которому осуществляется по принципу "первый вошел, первый вышел" /иногда сокращенно его называют методом доступа FIFO/. Элемент, который был первым поставлен в очередь, будет первым получен при поиске. Элемент, поставленный в очередь вторым, при поиске будет получен также вторым и т.д. Этот способ является единственным при постановке элементов в очередь и при поиске элементов в очереди. Применение очереди не позволяет делать прямой доступ к любому конкретному элементу.
В повседневной жизни очереди встречаются часто. Например, очередь в банке или очередь в кафетериях с быстрым обслуживанием являются очередью в указанном выше смысле /исключая те случае, когда человек пытается добиться обслуживания вне очереди!/. Для того, чтобы лучше понять работу очереди, рассмотрим две процедуры: постановка в очередь и выборка из очереди. При выполнении процедуры постановки в очередь элемент помещается в конец очереди. При выполнении процедуры выборки из очереди из нее удаляется первый элемент, который является результатом выполнения данной процедуры. Работа очереди проиллюстрирована на рис.1. Следует помнить, что при выборке из очереди из нее действительно удаляется один элемент. Если этот элемент нигде не будет сохранен, то в последствии к нему нельзя будет осуществить доступ.
Операция Содержимое очереди 1 Qstore(A) A 1 Qstore(B) A B 1 Qstore(C) A B C 2 Qretrieve returns A B C 1 Qstore(D) B C D 2 Qretrieve returns B C D 2 Qretrieve returns C D
Рис.1. Работа очереди: 1 - постановка в очередь; 2 - выборка из очереди элемента А, В, С.
Очереди в программировании используются во многих случаях, например, при моделировании (обсуждается ниже в соответствующей главе), при планировании работ (метод ПЕРТ или графики Гатта), при буферизации ввода-вывода.
В качестве примера рассмотрим простую программу планирования предписаний, которая позволяет обращаться к нескольким предписаниям. При каждом обращении предписание удаляется из списка и на экран выводится следующее предписание. Для простоты в программе используется массив символьных строк для управления событиями. Описание предписания ограничивается 80 символами и число предписаний не должно превышать 100. Прежде всего в этой программе планирования должны быть предусмотрены процедура постановки в очередь и процедура выборки из очереди. Эти процедуры приводятся ниже и даются необходимые описания глобальных переменных и типов данных.
const
MAX_EVENT = 100;
type
EvtType = string[80];
var
event: array[1..MAX_EVENT] of EvtType;
spos, rpos: integer;
{добавить в очередь}
procedure Qstore(q:EvtType);
begin
if spos=MAX_EVENT then
WriteLn('List full')
else
begin
event[spos]:=q;
spos:=spos+1;
end;
end; {конец процедуры постановки в очередь}
{ выборка объекта из очереди }
function Qretrieve:EvtType;
begin
if rpos=spos then
begin
WriteLn('No appointments scheduled.');
Qretrieve := ' ';
end else
begin
rpos:=rpos+1;
Qretrieve := event[rpos-1];
end;
end; { конец процедуры выборки из очереди }
В работе этих функций используются три глобальные переменные: "spos", которая содержит индекс следующего свободного элемента; "rpos", которая содержит индекс следующего выбираемого элемента и "event", которая представляет собой массив символьных строк с описанием предписаний. Переменные "spos" и "rpos" должны быть установлены в нулевое значение до первого обращения к процедурам постановки в очередь и выборки из очереди.
В этой программе процедура постановки в очередь помещает новые события в конец списка и делает проверку заполнения списка. Функция выборки из очереди выбирает события из очереди при необходимости их обработки. Когда планируется новое событие, переменная "spos" увеличивается на единицу, а когда событие завершается, то увеличивается на единицу переменная "rpos". Фактически переменная "rpos" преследует переменную "spos" в проходах по очереди. Этот процесс иллюстрируется на рис.2. Если значение указателя свободного места совпадает со значением указателя выбираемого элемента, то это означает, что в очереди нет событий. Следует помнить, что хотя функция выборки элемента из очереди в действительности не нарушает информацию в очереди, повторный доступ к ней невозможен и фактически она исчезает.
Ниже приводится целиком программа, осуществляющая простое планирование предписаниями. Вы можете усовершенствовать эту программу по собственному желанию.
Циклическая очередь
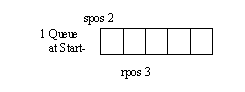
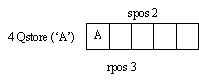
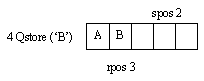
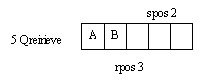
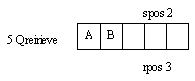
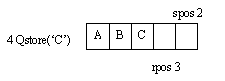
Рис.2. Указатель поиска преследует указатель свободного места в очереди:
1 - очередь в исходном положении;
2 - указатель свободного места в очереди;
3 - указатель следующего выбираемого элемента;
4 - процедура постановки в очередь;
5 - функция выборки из очереди.
{ простое планирование предписаниями }
procram MiniScheduler;
uses Grt;
const
MAX_EVENT = 100;
type
EvtType = string[80];
var
event: array[1..MAX_EVENT] of EvtType;
spos, rpos, t: integer;
ch:char;
done:boolean;
{ добавить в очередь }
procedure Qstore(q:EvtType);
begin
if spos=MAX_EVENT then
WriteLn('List full')
else
begin
event[spos] := q;
spos := spos+1;
end;
end; { конец процедуры постановки в очередь }
{ выборка объекта из очереди }
function Qretrieve:EvtType;
begin
if rpos=spos then
begin
WriteLn('No appointments scheduled.);
Qretrieve := ' ';
end else
begin
rpos := rpos+1;
Qretrieve := event[rpos-1];
end;
end; { конец функции выборки элемента из очереди }
{ ввести предписание в планировщик }
procedure Enter;
var
s: string[80];
begin
repeat
Write('Enter appointment',spos+1, ':');
ReadLn(s);
WriteLn;
if Length(s)<>0 then Qstore(s);
until Length(s)=0;
end; { конец процедуры ввода }
{ вывести предписание }
procedure Review;
var
t: integer;
begin
for t:=rpos to spos-1 do WriteLn(t+1,':',event[t]);
end; { конец процедуры вывода }
{ активизировать предписание }
procedure Periorm;
var
s:string[80];
begin
s:=Qretrieve; { получить следующее предписание }
if Length(s)<>0 then WriteLn(s);
end; { конец процедуры активизации предписаний }
begin { начало планировщика }
for t:= 1 to MAX_EVENT do event[t]:=''; { инициализация событий}
spos:=0; rpos:=0; done:=FALSE;
repeat
Write('Enter,Review, Pertorm,Quit: ');
ch:= ReadKey;
WriteLn;
Case upcase(ch) of
'E':Enter;
'R':Review;
'P':Perform;
'Q':done:=TRUE;
end;
until done=TRUE;
end.
При чтении предыдущего раздела вы возможно подумали об улучшении программы планирования предписаниями. Вместо остановки программы по достижению предела массива, который используется под очередь, можно указатель постановки в очередь и указатель выборки из очереди вернуть на начало массива. В этом случае в очередь можно добавлять любое число элементов в то время как элементы будут также выбираться из очереди. Такая очередь называется циклической, поскольку теперь массив используется не как линейный список, а как циклический список.
Для создания циклической очереди в программе планирования предписаний требуется изменить подпрограммы постановки в очередь и выборки из очереди следующим образом:
procedure Qstore(q: EvtType);
begin
{ убедитесь, что имеется свободное место в очереди }
if ((spos+1=rpos) or ((spos=MAX_EVENT) AND (rpos=0))then
WriteLn('List full')
else
begin
event[spos] := q;
spos := spos+1;
if spos=MAX_EVENT then spos:=1; { возврат в начало }
end;
end; { конец процедуры постановки в очередь }
function Qretrieve:EvtType;
begin
if rpos=MAX_EVENT then rpos:=1; { возврат в начало }
else rpos:=rpos+1;
if rpos=spos then
begin
WriteLn('Queue empty');
Qretrieve:=';';
end else
Qretrieve:=event[rpos-1];
end; { конец функции выборки из очереди }
В действительности очередь становится заполненной только в том случае, когда указатель свободного места совпадает с указателем выборки следующего элемента. В противном случае очередь будет иметь свободное место для нового элемента. Однако, это значит, что в начале программы индекс выборки должен устанавливаться не в нулевое значение, а на значение максимального числа событий. В противном случае первое обращение к процедуре постановки в очередь приведет к появлению сообщения о заполнении списка. Следует помнить, что очередь может содержать только на один элемент меньше, чем значение максимального числа событий, поскольку указатели выборки и постановки в очередь всегда должны отличаться хотя бы на единицу (в противном случае нельзя будет понять заполнена ли очередь или она пустая).
Наиболее широко циклические очереди применяются в операционных системах при буферизации информации, которая считывается или записывается на дисковые файлы или консоль. Другое широкое применение эти очереди нашли в решении задач реального времени, когда, например, пользователь может продолжать делать ввод с клавиатуры во время выполнения другой задачи. Так работают многие текстовые процессоры, когда изменяется формат параграфа или выравнивается строка. Имеется короткий промежуток времени, когда набранная на клавиатуре информация не выводится на экран до окончания другого процесса. Для достижения такого эффекта в программе должна предусматриваться постоянная проверка ввода с клавиатуры в ходе выполнения другого процесса. При вводе некоторого символа его значение должно быстро ставиться в очередь и процесс должен продолжаться. После завершения процесса набранные символы выбираются из очереди и обрабатываются обычным образом.
Для того, чтобы понять, как это можно сделать с помощью циклической очереди, рассмотрим следующую простую программу, состоящую из двух процессов. Первый процесс выполняет подсчет до 32 000. Второй процесс устанавливает символы в циклическую очередь по мере того как они вводятся с клавиатуры. При этом вводимые символы не будут выводиться на экран до тех пор, пока не будет введена точка с запятой. Вводимые символы не будут выводиться на экран, поскольку первый процесс будет иметь более высокий приоритет до тех пор, пока вы не введете точку с запятой или пока счетчик не достигнет максимального значения. Затем из очереди будут выбраны введенные символы и выведены на экран.
{ программа, иллюстрирующая применение циклической очереди }
program KeyBuffer;
uses Crt, Dos;
const
MAX_EVENT = 10;
type
EvtType = char;
var
event: array[1..MAX_EVENT] of EvtType;
spos, rpos, t: integer;
ch: char;
{ поместить объект в очередь }
procedure Qstore(q:EvtType);
begin
2 { убедиться, что в очереди имеется свободное место}
if ((spos+1=rpos) or ((spos=MAX_EVENT) AND (rpos=0))then
WriteLn('List full')
else
begin
event[spos]:=q;
spos:=spos+1;
if spos=MAX_EVENT then spos:=1; { вернуться в начало очереди }
end;
end; { конец процедуры постановки в очередь }
{ выборка объекта из очереди }
function Qretrieve:EvtType;
begin
if rpos=MAX_EVENT then rpos:=1; { вернуться в начало очереди }
else rpos:=rpos+1;
if rpos=spos then
begin
WriteLn('Queue empty');
Qretrieve:=';';
end else
begin
Qretrieve:= event[rpos-1];
end;
end; { конец функции выборки объекта из очереди }
begin { буфер набранных с помощью клавиатуры символов }
spos := 0;
rpos := MAX_EVENT;
{ установить переменную "ch" на начальное значение, отличное от точки с запятой }
ch:=' ';
t := 1;
repeat
if KeyPressed then
begin
ch := ReadKey;
Qstore(ch);
end;
t:=t+1;
write(t); write(' ');
until (t=32000) or (ch=';');
{ вывести содержимое буфера введенных с клавиатуры символов }
repeat
ch:=Qretrieve;
if ch<>';' then Write(ch);
until ch = ';';
end.
Процедура "KeyPressed" делает обращение к программе операционной системы, которая возвращает значение "истина", если была нажата какая-либо клавиша, или значение "ложь", если клавиатура не использовалась.
СТЕКИ
Организация стека в определенном смысле противоположна организации очереди, поскольку здесь используется доступ по принципу "последней вошел, первый вышел" /такой метод доступа иногда называют методом LIFO/. Представим себе стопку тарелок. Нижняя тарелка из этой стопки будет использована последней, а верхняя тарелка /которая была установлена в стопку последней/ будет использована первой. Стеки широко используются в системном программном обеспечении, включая компиляторы и интерпретаторы.
Исторически сложилось так, что две основные операции для стека - поместить в стек и выбрать из стека - получили название соответственно "затолкнуть" и "вытолкнуть". Поэтому для реализации стека необходимо создать две функции: "posh" /затолкнуть/, которая помещает элемент в вершину стека, и "pop" /вытолкнуть/, которая выбирает из вершины стека значение. Необходимо также предусмотреть определенную область в памяти, где фактически будет храниться стек. Для этого можно использовать массив или можно выделить область памяти, используя средство динамического распределения памяти, предусмотренное в языке Паскаль. Как и при работе с очередью при выборке значения из стека элемент будет потерян, если его не сохранить где-нибудь в памяти. Ниже приводится общая форма процедур установки в стек и выборки из стека.
const
MAX = 100;
var
stack:array[1..100] of integer;
tos:integer; {points to top of stask}
{ помещение объекта в стек }
procedure Push(i:integer);
begin
if tos>=MAX then WriteLn('Stask full')
else
begin
stack[tos]:=i;
tos:=tos+1;
end;
end; { конец процедуры помещения объекта в стек}
{ выборка объекта из стека }
function Pop:integer;
begin
tos:=tos-1;
if tos<1 then
begin
WriteLn('Stack underflow');
tos:=tos+1;
Pop:=0;
end
else Pop := stack[tos];
end; { конец функции выборки объекта из стека }
Переменная "tos" содержит значение индекса для следующего помещаемого в стек элемента. При реализации этих процедур никогда нельзя забывать о проверке ситуаций переполнения стека и выборки из пустого стека. В приведенных процедурах нулевое значение указателя "tos" означает, что стек пуст, а значение этого указателя, равное или превышающее адрес последней ячейки памяти, где содержится стек, означает заполнение стека. Рис.3 иллюстрирует работу стека.
Операция Содержимое стека Push(A) A Push(B) B A Push(C) C B A Pop, выбирается С В А Push(F) F B A Pop, выбирается F B A Pop, выбирается В А Рор, выбирается А пусто
Рис.3. Работа стека.
Хорошим примером применения стека является калькулятор, который может выполнять четыре действия. Большинство калькуляторов используют стандартную форму выражений, которая носит название инфиксной формы. В общем виде ее можно представить в виде "операнд-оператор-операнд". Например, для прибавления 100 к 200 вы должны ввести число 100, набрать символ сложения, ввести число 200 и нажать клавишу со знаком равенства. Однако, некоторые калькуляторы применяют другую форму выражений, получившую название постфиксной формы. В этом случае оба операнда вводятся перед вводом оператора. Например, для добавления 100 к 200 при использовании постфиксной формы сначала вводится число 100, затем вводится число 200 и после этого нажимается клавиша со знаком плюс. Введенные операнды помещаются в стек. При вводе оператора из стека выбираются два операнда и результат помещается в стек. При использовании постфиксной формы очень сложные выражения могут легко вычисляться на калькуляторе.
Ниже показана программа для такого калькулятора.
{ калькулятор с четырьмя операциями, иллюстрирующий работу }
program four_function_calc;
const
MAX = 100;
var
stack:array [1..100] of integer;
tos:integer; { указатель вершины стека }
a, b:integer;
s:string[80];
{ поместить объект в стек }
procedure Push(i:integer);
begin
if tos >= MAX then Writeln('Stack full')
else
begin
stack[tos] :=1;
tos := tos+1;
end;
end;{Push}
{ выборка объекта из стека }
function Pop:integer;
begin
tos := tos-1;
if tos < 1 then
begin
Writeln('Stack underflow')
tos := tos+1;
Pop := 0;
end
else Pop := stack[tos];
end;{ Pop }
begin { калькулятор }
tos := 1;
Writeln('For Function Calculator');
repeat
Write(': '); { вывод приглашения }
Readln(s);
Val(s, a, b) { преобразование строки символов в целое число }
{ считается, что при успешном преобразовании пользователь ввел число, а
в противном случае пользователь ввел оператор}
if (b=0) and ((Length(s)>1) or (s[1]<>'-')) then
Push(a)
else
case s[1] of
'+' begin
a := Pop
b := Pop
Writeln(a+b);
Push(a+b);
end;
'-' begin
a := Pop
b := Pop
Writeln(b+a);
Push(b+a);
end;
'*' begin
a := Pop
b := Pop
Writeln(a*b);
Push(a*b);
end;
'/' begin
a := Pop
b := Pop
if a=0 then Writeln('divide by zero');
else
begin
Writeln(b div a);
Push(b div a);
end;
end;
'.' begin
a := Pop
Writeln(a);
Push(a);
end;
end;
until UpCase(s[1])='G'
end.
Для того, чтобы посмотреть, что находится в вершине стека, достаточно ввести точку. Хотя данная программа выполняет арифметические действия только с целыми числами, ее легко можно приспособить для чисел с плавающей запятой, изменяя тип данных стека и преобразуя оператор "div" в оператор деления для чисел с плавающей запятой /наклонная черта/.
СВЯЗАННЫЕ СПИСКИ
Очереди и стеки обладают двумя общими свойствами. Во-первых, доступ к находящимся в них данных подчиняется строгим правилам. Во-вторых, операции поиска имеют разрушительный характер. Если выбранный из стека или очереди элемент не будет где-нибудь сохранен, то он будет потерян. Кроме того, стеки и очереди для своей работы требуют наличия непрерывной области памяти /непрерывность должна обеспечиваться по крайней мере логически/.
В отличии от стека и очереди связанный список позволяет осуществлять доступ к любым элементам, поскольку каждая единица информации имеет указатель на следующий элемент данных в цепочке. Элементами связанного списка являются сложные структуры данных, тогда как стеки и очереди могут работать и с простыми и со сложными структурами данных. Операция поиска в связанном списке не приводит к удалению и уничтожению элемента. В данном случае следует предусмотреть дополнительно операцию удаления элемента из списка.
Связанные списки используются в двух основных случаях. Во-первых, при создании массивов, которые располагаются в оперативной памяти и размер которых заранее неизвестен. Если вы заранее знаете, какого размера память потребуется для решения вашей задачи, то вы можете использовать простой массив. Однако, если действительный размер списка вам неизвестен, то вы должны применить связанный список. Во-вторых, связанные списки используются в базах данных на дисках. Связанный список позволяет быстро выполнять вставку и удаление элемента данных без реорганизации всего дискового файла. По этим причинам связанные списки широко используются в программах по управлению базами данных.
Связанные списки могут иметь одиночные или двойные связи. Список с одной связью содержит элементы, каждый из которых имеет связь со следующим элементом данных. В списке с двойной связью каждый элемент имеет связь как со следующим элементом, так и с предыдущим элементом. Тип связанного списка выбирается в зависимости от решаемой задачи.
Связанные списки с одиночной связью
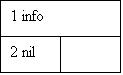
В списке с одиночной связью каждый элемент данных имеет связь с последующим элементом в списке. Каждый элемент данных обычно представляет собой запись, которая содержит информационные поля и указатель связи. Список с одиночной связью показан на рис.4.
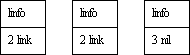
Рис.4. Расположение списка с одиночной связью в памяти:
1 - информация;
2 - указатель связи;
3 - нуль.
Имеется два способа построения списка с одиночной связью. В первом случае каждый новый элемент добавляется в начало или в конец списка. Во втором случае каждый элемент добавляется в свое место в списке /например, так, чтобы обеспечить упорядочность по возрастанию/.
Способ построения списка определяется процедурой постановки нового элемента в список. Ниже дается такая процедура для простого случая, когда элементы добавляются в конец списка. Необходимо определить запись, которая будет содержать информацию и указатели связи. В этом примере запись содержит адрес почтовой корреспонденции. Тип записи для каждого элемента в списке адресов определяется ниже:
AddrPointer = ^address;
address = record
name: string[30];
street: string[40];
city: string[20];
state: string[2];
zip: string[9];
next: AddrPointer; { указатель на следующую запись }
end;
DataItem = address;
var
start.last: AddrPointer;
Ниже представлена функция добавления в список с одной связью, когда каждый новый элемент помещается в конец списка. Указатель записи типа "address" должен передаваться в качестве аргумента функции:
{ добавление в список с одной связью }
procedure SL_Store(i: AddrPointer);
Legin
if last=nil then { первый элемент списка } 2
begin
last := i;
start := i;
i^.next := nil;
end else
begin
last^.next := i;
i^.next := nil;
last := i;
end;
end; { конец процедуры добавления элементов в список с одной связью }
Следует помнить, что до первого обращения к этой функции переменные "start" и "last" должны быть установлены на значение "nil".
Можно предусмотреть отдельную операцию по сортировке списка, созданного с помощью указанной функции добавления элементов в список с одной связью. Однако упорядочения легче добиться во время вставки путем установки каждого нового элемента в соответствующее место списка. Кроме того, если список уже является отсортированным, то имеет смысл сохранить его упорядоченность, вставляя каждый новый элемент в соответствующее место списка. Для этого делается последовательный просмотр списка до тех пор, пока не будет найдено нужное место. В это место вставляется новый адрес и делается соответствующее изменение связей.
При вставке элемента в список с одной связью может возникнуть одна из трех ситуаций. Во-первых, новый элемент может оказаться первым в списке. Во-вторых, он может встать между другими двумя элементами и в-третьих, он может оказаться последним элементом в списке. На рис.5 показано, как для каждого из этих случаев изменяются связи.
Если изменяется первый элемент списка, то везде в программе должна быть изменена точка входа в список. Для того, чтобы избежать этого, в качестве первого элемента нужно использовать фиктивный элемент. Этот фиктивный элемент должен иметь такое значение, которое обеспечивает ему первое место в списке. В этом случае точка входа в список не будет меняться. Однако, недостатком такого метода является необходимость расхода дополнительной памяти для фиктивного элемента и поэтому в показанном примере этот метод не используется.
| 1 Новый первый элемент | |

|

|
| 4 becomes | |

|

|
| 6 New Middle Item | |

|

|
| 4 becomes | |

|

|
| 7 New Last Item | |

|
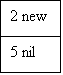
|
| 4 becomes | |

|

|
Рис.5. Вставка элемента в список с одной связью: 1 - новый первый элемент; 2 - новый элемент; 3 - информационные поля; 4 - справа дается преобразованный список; 5 - нулевой указатель связи; 6 - новый средний элемент; 7 - новый последний элемент.
Приводимая ниже функция используется для вставки адресов почтовых корреспонденций в порядке возрастания фамилий /поле "name"/. В качестве результата функции выдается первый элемент списка. Входными аргументами этой функции являются указатели на начало и конец списка.
{ добавление элементов в список с одной связью с сохранением упорядоченности }
function SLS_Store(info, start: AddrPointer;
var last: AddrPointer): AddrPointer;
var
old, top: AddrPointer;
done: boolean;
begin
top := start;
old := nil;
done := FALSE;
if start=nil then
begin { первый элемент списка }
info^.next:=nil;
ast:=info;
SLS_Store:=info;
end else
begin
while (start<>nil) and (not done) do
begin
if start^.name < info^.name then
begin
old:=start;
start:=start^.next;
end else
begin { вставка в середину }
if old<>nil then
begin
old^.next:=info;
info^.next:=start;
SLS_Store:=top; { сохранить начало }
done:=TRUE;
end else
begin
info^.next:=start; { новый первый элемент }
SLS_Store:=info;
done:=TRUE;
end;
end;
end; {while}
if not done then
begin
last^.next:=info; { вставка в конец }
info^.next:=nil;
last:=info;
SLS_Store:=top;
end;
end;
end;
{ конец процедуры упорядоченной вставки в список с одной связью}
Для связанного списка обычно не предусматривается отдельная функция, связанная с процессом поиска, при котором элементы выдаются в порядке их расположения в списке. Эта функция обычно программируется очень просто и оформляется вместе с другими функциями, например, поиском отдельного элемента, его удалением или выводом на экран. В качестве примера ниже приводится процедура вывода всех фамилий в списке адресов почтовых корреспонденций:
procedure Display(start: AddrPointer);
begin
while start<>nil do begin
WriteLn(start^.name);
start:=start^.next;
end;
end; { конец процедуры вывода}
Здесь переменная "start" является указателем на первую запись в списке.
Поиск элемента в списке представляет собой простую процедуру прохода по цепочке. Процедуру поиска адресов по фамилиям можно составить следующим образом:
function Search(start:AddrPointer;name:str80):AddrPointer;
var
done:boolean;
begin
done := FALSE;
while (start<>nil) and (not done) do
begin
if name=start^.name then
begin
Search:=start;
done:=TRUE;
end else
start:=start^.next;
end;
if start=nil then Search := nil; { нет в списке }
end; { конец процедуры поиска элемента }
Поскольку эта процедура поиска в результате выдает указатель на тот элемент списка, который соответствует искомой фамилии, переменная "Search" должна объявляться как указатель записи типа "address". Если требуемый элемент отсутствует в списке, то в результате выдается нулевой указатель.
Процедура удаления элемента из списка с одной связью программируется просто. Как при вставке элемента здесь может встретиться один из трех случаев: удаляется первый элемент, удаляется средний элемент и удаляется последний элемент. На рис.6 иллюстрируется каждая ситуация.
| 1 Deleting the First Item | 2 becomes |

|

|
| 6 Deleting a Middle Item | 2 becomes |

|

|
| 7 Deleting the Last Item | 2 becomes |

|

|
Рис.6. Удаление элемента из списка с одной связью: 1 - удаление первого элемента; 2 - левый список преобразуется в правый; 3 - информационные поля; 4 - удаленный элемент; 5 - связь с нулевым значением; 6 - удаление среднего элемента; 7 - удаление последнего элемента.
Приводимая ниже функция выполняет удаление заданного элемента из списка записей адресов:
function SL_Delete(start, item, prior_item: AddrPointer):AddrPointer;
begin
if prior_item<>nil then
prior_item^.next:=item^.next
else start:= item^.next;
SL_Delete:=start;
end; { конец функции удаления элемента из списка с одной связью }
Приведенная функция передает указатель элемента, указатель элемента, стоящего перед удаленным, и указатель на начало списка. Если удаляется первый элемент, то указатель элемента, стоящего перед удаленным, будет иметь нулевое значение. Значением функции должен являться указатель на начало списка, поскольку может удалиться первый элемент и необходимо знать, где будет новый первый элемент списка.
Списки с одной связью имеют один большой недостаток, который препятствует их широкому применению: такой список нельзя просматривать в обратном направлении. Для этих целей используются списки с двойной связью.
Списки с двойной связью
Каждый элемент в списке с двойной связью имеет указатель на следующий элемент списка и указатель на предыдущий элемент списка. Рис.7 иллюстрирует характер связей в таком списке. Список, который вместо одной имеет две связи, отличается двумя основными преимуществами. Во-первых, список может читаться в обоих направлениях. Это не только упрощает сортировку списка, но также позволяет пользователям базы данных просматривать данные в обоих направлениях. Во-вторых, и прямая и обратная связь позволяют прочитать список полностью и поэтому при нарушении одной из связей список может быть восстановлен по другой связи. Это свойство имеет смысл использовать при отказах оборудования, приводящих к нарушению списка.
|

|
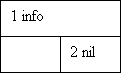
|
Рис.7. Список с двойной связью: 1 - информационные поля; 2 - связь с нулевым значением.
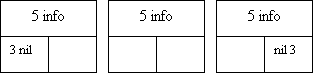
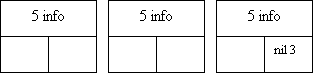
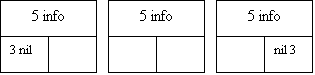
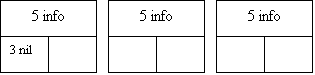
Для списка с двойной связью предусматриваются три основные операции: вставка нового первого элемента, вставка нового среднего элемента и вставка нового последнего элемента. Эти операции проиллюстрированы на рис.8.
Список с двойной связью строится подобно списку с одной связью, причем в записи должно быть предусмотрено место для двух указателей. Для примера со списком почтовых корреспонденций запись адреса можно модифицировать следующим образом:
type str80 = string[80]; AddrPointer = ^address; address = record
| 1 Inserling a New First Element | |

|

|
| 4 becomes | |
|
|
| 6 Inserling a New Middle Element | |

|

|
| 4 becomes | |

|
|
| 7 Inserling a New Last Element | |

|

|
| 4 becomes | |

|
|
Рис.8. Вставка элемента в список с двойной связью: 1 - вставка нового первого элемента; 2 - новый элемент; 3 - указатель с нулевым значением; 4 - левый список преобразуется в правый; 5 - информационные поля; 6 - вставка нового среднего элемента; 7 - вставка нового последнего элемента.
name : string[30];
street: string[40];
city: string[20];
state: string[2];
zip: string[9];
next: AddrPointer; { указатель на следующую запись }
prior: AddrPointer; { указатель на предыдущую запись }
end;
DataItem = address;
DataArray = array [1..100] of AddrPointer;
Ниже приводится функция, которая позволяет строить список с двойной связью для записей адресов:
{добавление элементов в список с двойной связью }
procedure DL_Store(i: AddrPointer);
begin
if last=nil then { первый элемент списка }
begin
last:=i;
start:=i;
i^.next:=nil;
i^.prior:=nil;
end
else
begin
last^.next:=i;
i^.next:=nil;
i^.prior:=last;
last:=i;
end;
end; { конец функции добавления в список с двойной связью }
Эта функция помещает каждый новый элемент в конец списка. Следует иметь в виду, что перед первым обращением к функции переменные "start" и "last" должны устанавливаться в нулевое значение.
В ходе построения списка с двойной связью каждый новый элемент может /как и для списка с одной связью/ устанавливаться не в конец, а в соответствующее место, обеспечивая упорядочность элементов в списке. Ниже приводится функция, которая создает список с двойной связью, упорядоченый по возрастанию фамилий из записей адресов:
{упорядоченная установка элементов в список с двойной связью}
function DSL_Store(info, start: AddrPointer;
var last: AddrPointer): AddrPointer;
{ вставка элементов в соответствующее место с сохранением порядка }
var
old, top: AddrPointer;
done: boolean;
begin
top := start;
old := nil;
done := FALSE;
if start = nil then begin { первый элемент списка }
info^.next := nil;
last := info;
info^.prior :=nil;
DCL_Store := info;
end else
begin
while (start<>nil) and (not done) do
begin
if start^.name < info^.name then
begin
old := start;
start := start^.next;
end else
begin { вставка в середину }
if old <>nil then
begin
old^.next := info;
info^.next := start;
start^.prior := info;
info^.prior := old;
DSL_Store := top; { сохранение начала }
done := TRUE;
end else
begin
info^.next := start;{новый первый элемент }
info^.prior := nil;
DSL_Store := info;
done := TRUE;
end;
end;
end; { конец цикла }
if not done then begin
last^.next := info;
info^.next := nil;
info^.prior := last;
last := info;
DSL_Store := top; { сохранение начала }
end;
end;
end; { конец функции DSL_Store }
Поскольку элемент может помещаться в самое начало списка, эта функция должна выдавать указатель на начало списка, чтобы в других частях программы учесть изменения начала списка. При поиске конкретного элемента списка, как и для списка с одиночной связью, делается последовательный проход по цепочке связей пока не будет найден требуемый элемент.
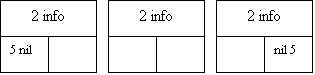
При удалении элемента из списка возникает одна из трех ситуаций: удаление первого элемента, удаление среднего элемента и удаление последнего элемента. Рис.9 иллюстрирует изменение связей для этих случаев.
| 1 Deleting the First Item | |
| 3 becomes | |
|
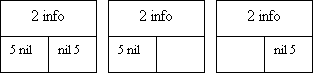
|
| 6 Deleting a Middle Item | |
| 3 becomes | |

|
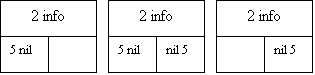
|
| 7 Deleting the Last Item | |
| 3 becomes | |

|
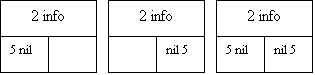
|
Рис.9. Удаление элемента из списка с двойной связью: 1 - удаление первого элемента; 2 - информационные поля; 3 - левый список преобразуется в правый; 4 - удаленный элемент; 5 - указа- тель с нулевым значением; 6 - удаление среднего элемента; 7 - удаление последнего элемента.
Ниже приводится функция, которая выполняет удаление элемента типа "address" из списка с двойной связью:
{ удаление элемента из списка с двойной связью }
function DL_Delete(start: AddrPointer;
key: str80): AddrPointer;
var
temp, temp2: AddrPointer;
done: boolean;
begin
if start^.name=key then begin { первый элемент списка}
DL_Delete:=start^.next;
if temp^.next <> nil then
begin
temp := start^.next;
temp^.prior := nil;
end;
dispose(start);
end else
begin
done := FALSE;
temp := start^.next;
temp2 := start;
while (temp<>nil) and (not done) do
begin
if temp^.name=key then
begin
temp^.next:=temp^.next;
if temp^.next<>nil then
temp^.next^.prior:=temp2;
done:=TRUE;
dispose(temp);
end else
begin
temp2:=temp;
temp:=temp^.next;
end;
end;
DL_Delete:=start; { начало не изменяется }
if not done then WriteLn('not found');
end;
end; { конец функции удаления элемента из списка с двойной связью }
Этой функции передается на один указатель меньше, чем для соответствующей функции при использовании списка с одной связью. /Удаленный элемент уже имеет указатель на предыдущий элемент и указатель на следующий элемент/. Поскольку первый элемент в списке может измениться, функция возвращает указатель на начало списка.
Список адресов почтовых корреспонденций, построенный в виде списка с двумя связями
Ниже приведена простая программа для списка почтовых корреспонденций, построенного в виде списка с двойной связью. Здесь весь список содержится в оперативной памяти. Однако, программа может быть изменена для хранения списка на диске.
{простая программа для списка адресов почтовых корреспонденций,
иллюстрирующая применение списков с двойной связью}
program mailing_list;
type
str80 = string[80];
AddrPointer = ^address;
address = record
name: string[30];
street: string[40];
city: string[20];
state: string[2];
zip: string[9];
next: AddrPointer; { указатель на следующую запись }
prior: AddrPointer; { указатель на предыдущую запись }
end;
DataItem = address;
filtype = file of address;
var
t, t2: integer;
mlist: FilType;
start, last: AddrPointer;
done: boolean;
{ вызов меню }
function MenuSelect: char;
var
ch: char;
begin
Writeln('1. Enter names');
Writeln('2. Delete a name');
Writeln('3. Display the list');
Writeln('4. Search for a name');
Writeln('5. Save the list');
Writeln('6. Load the list');
Writeln('7. Quit');
repeat
Writeln;
Write('Enter your choice: ');
Readln(ch);
ch := UpCase(ch);
until (ch>='1') and (ch<='7')
MenuSelect := ch;
end;{ конец выбора по меню }
{ упорядоченная установка элементов в список с двойной связью }
function DSL_Store(info, start: AddrPointer;
var last: AddrPointer): AddrPointer;
{ вставка элементов в соответствующее место с сохранением порядка }
var
old, top: AddrPointer;
done: boolean;
begin
top := start;
old := nil;
done := FALSE;
if start = nil then begin { первый элемент списка }
info^.next := nil;
last := info;
info^.prior :=nil;
DSL_Store := info;
end else
begin
while (start<>nil) and (not done) do
begin
if start^.name < info^.name then
begin
old := start;
start := start^.next;
end else
begin { вставка в середину }
if old <>nil then
begin
old^.next := info;
info^.next := start;
start^.prior := info;
info^.prior := old;
DSL_Store := top; { сохранение начала }
done := TRUE;
end else
begin
info^.next := start;{новый первый элемент }
info^.prior := nil;
DSL_Store := info;
done := TRUE;
end;
end;
end; { конец цикла }
if not done then begin
last^.next := info;
info^.next := nil;
info^.prior := last;
last := info;
DSL_Store := top; { сохранение начала }
end;
end;
end; { конец функции DSL_Store }
{ удалить элемент из списка с двойной связью }
function DL_Delete(start: AddrPointer
key: str[80]): AddrPointer
var
temp, temp2: AddrPointer
done: boolean;
begin
if star^.name = key then begin { первый элемент списка }
DL_Delete := start^.next;
if temp^.next <> nil then
begin
temp := start^.next;
temp^.prior := nil;
end;
dispose(start);
end else
begin
done := FALSE;
temp := start^.next;
temp2 := start;
while (temp <> nil) and (not done) do
begin
if temp^.next <> nil then
temp^.next^.prior := temp2
done := TRUE
dispose(temp);
end else
begin
temp2 := temp;
temp := temp^.next;
end;
end;
DL_Delete := start; { начало не изменяется }
if not done then Writeln('not found');
end;
end; { конец функции DL_Delete }
{ удаление адреса из списка }
procedure remove;
var
name:str80;
begin
Writeln('Enter name to delete: ');
Readln(name);
start := DL_Delete(start,name);
end; { конец процедуры удаления адреса из списка }
procedure Enter;
var
info: AddrPointer;
done: boolean;
begin
done := FALSE;
repeat
new(info) { получить новую запись }
Write('Enter name: ');
Readln(info^.name);
if Length(info^.name)=0 then done := TRUE
else
begin
Write(Enter street: ');
Readln(info.street);
Write(Enter city: ');
Readln(info.city);
Write(Enter state: ');
Readln(info.state);
Write(Enter zip: ');
Readln(info.zip);
start := DSL_Store(info, start, last); { вставить запись }
end;
until done;
end; { конец ввода }
{ вывести список }
procedure Display(start:AddrPointer);
begin
while start <> nil do begin
Writeln(start^.name);
Writeln(start^.street);
Writeln(start^.city);
Writeln(start^.state);
Writeln(start^.zip);
start := start^.next
Writeln;
end;
end;
{ найти элемент с адресом }
function Search(start: AddrPointer; name: str80):
AddrPointer;
var
done: boolean;
begin
done := FALSE
while (start <> nil) and (not done) do begin
if name = start^.name then begin
search := start;
done := TRUE;
end else
start := star^.next;
end;
if start = nil then search := nil; { нет в списке }
end; { конец поиска }
{ найти адрес по фамилии }
procedure Find;
var
loc: Addrpointer;
name: str80;
begin
Write('Enter name to find: ');
Readln(name);
loc := Search(start, name);
if loc <> nil then
begin
Writeln(loc^.name);
Writeln(loc^.street);
Writeln(loc^.city);
Writeln(loc^.state);
Writeln(loc^.zip);
end;
else Writeln('not in list')
Writeln;
end; { Find }
{ записать список на диск }
procedure Save(var f:FilType; start: AddrPointer):
begin
Writeln('saving file');
Rewrite(f);
while start <> nil do begin
write(f,start);
start := start^.next;
end;
end;
{ загрузить список с файла }
procedure Load(var f:FilType; start: AddrPointer):
AddrPointer;
var
temp, temp2: AddrPointer
first: boolean;
begin
Writeln('load file');
Reset(f);
while start <> nil do begin { освобождение памяти при необходимости }
temp := start^.next
dispose(start);
start := temp;
end;
start := nil; last := nil;
if not eof(f) then begin
New(temp);
Read(i, temp^);
temp^.next := nil; temp^.prior:= nil;
load := temp; { указатель на начало списка }
end;
while not eof(f) do begin
New(temp2);
Read(i, temp2^);
temp^.next := temp2; { построить список }
temp2^.next := nil;
temp^.prior := temp2;
temp := temp2;
end;
last := temp2;
end; { конец загрузки }
begin
start := nil; { сначала список пустой }
last := nil;
done := FALSE;
Assign(mlist, 'mlistd.dat');
repeat
case MenuSelect of
'1': Enter;
'2': Remove;
'3': Display(start);
'4': Find;
'5': Save(mlist, start);
'6': start := Load(mlist, start);
'7': done := TRUE;
end;
until done=TRUE;
end. { конец программы }
ДВОИЧНЫЕ ДЕРЕВЬЯ
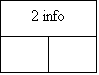
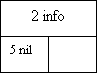
В этом разделе рассматривается четвертая структура данных, которая называется двоичным деревом. Имеется много типов деревьев. Однако, двоичные деревья занимают особое положение. Если такие деревья упорядочить, то операции поиска, вставки и удаления будут выполняться очень быстро. Каждый элемент двоичного дерева имеет информационные поля, связь с левым элементом и связь с правым элементом. На рис.10 показано небольшое дерево.
При описании деревьев используется специальная терминология. Первый элемент дерева называется его корнем. Каждый элемент называют вершиной /или листом/ дерева, а часть дерева носит название поддерева. Вершина, которая не имеет поддеревьев, называется терминальной вершиной. Высота дерева равна числу уровней вершин в дереве. В дальнейшем при рассмотрении деревьев можно считать, что в памяти они располагаются так же, как на бумаге. Однако следует помнить, что деревья представляют собой лишь способ представления данных в памяти, а память в действительности имеет линейную форму.
| Root Node 1 | ||||
 |
||||
| 3 | 4 | |||
| Left Subtree | Right Subtree | |||
 |
 |
|||
 |
 |
 |
||
| 6 | ||||
| Terminal Nodes | ||||
Рис.10. Пример двоичного дерева: 1 - корневая вершина; 2 - информационные поля; 3 - левое поддерево; 5 - указатель связи с нулевым значением; 6 - терминальные вершины.
Двоичное дерево представляет собой особую форму связанного списка. Доступ к элементам, их вставка и удаление могут выполняться в любом порядке. Кроме того, операция поиска не носит разрушительный характер. Хотя деревья легко представляются образно, для программирования они представляют достаточно непростую задачу.
Большинство функций над деревьями носят рекурсивный характер, поскольку дерево само по себе является рекурсивной структурой данных. /Т.е. каждое поддерево само является деревом/. Поэтому представленные в этом разделе программы являются, как правило, рекурсивными. Имеются нерекурсивные версии этих функций, однако разобраться в них значительно труднее.
Упорядоченность дерева зависит от порядка доступа к дереву. Процесс доступа к каждой вершине дерева называется обходом дерева.
Имеется три способа обхода дерева: во внутреннем порядке, в прямом порядке и в обратном порядке. При прохождении дерева во внутреннем порядке сначала посещается левое поддерево, затем корень и затем посещается правое дерево. При прохождении дерева в прямом порядке сначала посещается корень, затем левое поддерево и затем правое поддерево. При прохождении дерева в обратном порядке сначала посещается левое поддерево, затем правое поддерево и затем корень.
Порядок прохождения ds, выбранного в качестве примера дерева будет следующим:
при прохождении во внутреннем порядке: a b c d e f g; при прохождении в прямом порядке: d b a c f e g; при прохождении в обратном порядке: a c b e g f d.
Хотя дерево не обязательно должно быть упорядочено, в большинстве случаев оно должно быть таким. Упорядоченность дерева зависит от того, как вы будете проходить дерево. В приводимых ниже примерах используется внутренний порядок прохода по дереву. В отсортированном двоичном дереве левое поддерево содержит вершины, которые меньше или равны корню, а вершины правого поддерева больше или равны корню. Ниже приводится функция, которая выполняет построение отсортированного двоичного дерева:
type
TreePointer = ^tree;
tree = record
data: char;
left: TreePointer;
right:TreePointer;
end;
{ добавить элемент в двоичное дерево }
function Stree(root,r:TreePointer;data:char);TreePointer;
begin
if r=nil then
begin
new(r); { получить новую вершину }
r^.left:=nil;
r^right:=nil;
r^.data:=data;
if data<root^.data then root^.left:=r
else root^.right:=r;
STree:=r;
end else
begin
if datar^.data then STree:=STree(r, r^.left, data)
else STree:=STree(r, r^.right, data);
end;
end; { конец функции добавления элемента в двоичное дерево }
В этом алгоритме выполняется просто прохождение по связям дерева, двигаясь вправо или влево в зависимости от поля данных. При применении этой функции необходимо предусмотреть глобальную переменную для корня дерева. Вначале эта глобальная переменная должна быть установлена в нулевое значение. Указатель на корень будет установлен при первом обращении к указанной функции. Поскольку при последующих обращениях к этой функции нет необходимости делать новую установку корня, то используется фиктивная переменная. Если глобальной переменной будет "rt", то обращение к указанной функции может иметь следующий вид:
{call STree}
if rt=nil rt:=STree(rt, rt, info)
else dummy := STree(rt, rt, info);
При таком обращении к функции вставка и первого и последующих элементов будет выполняться корректно.
Указанная функция является рекурсивной, как и большинство других процедур с деревьями. Если этот алгоритм преобразовать, используя прямой метод перехода рекурсивных алгоритмов в циклиескую форму, то программа будет в несколько раз длинее. При обращении к функции задается указатель на корень и указатель на поддерево, а также помещаемые в дерево данные. Здесь в качкестве вставляемых в дерево данных используется символьное данное. Однако, в качестве такого данного можно использовать данное любого типа.
Для обхода дерева с использованием указанной функции и выдачи на печать поля данных каждой вершины можно использовать следующую функцию:
procedure InOrder(root:TreePointer);
begin
if root>nil then
begin
InOrder(root^.left);
Write(root^.data);
InOrder(root^.right);
end;
end.
Эта функция делает обход дерева во внутреннем порядке и завершается при обнаружении терминального листа /указателя о нулевом завершении/. Ниже показаны функции для прохождения дерева в прямом и обратном порядке:
procedure PreOrder(root:TreePointer);
begin
if root<>nil then
begin
write(root^.data);
preorder(root^.left);
preorder(root^.right);
end;
end.
procedure PostOrder(root:TreePointer);
begin
if root<>nil then
begin
postorder(root^.left);
postorder(root^.right);
Write(root^.data);
end;
end.
Вы можете составить короткую программу, которая строит упорядоченное двоичное дерево и, кроме того, печатает его на экране вашего компьютера. Для этого требуется выполнить лишь незначительные изменения в процедуре прохода дерева во внутреннем порядке. Ниже приводится программа, которая выдает вершины дерева во внутреннем порядке:
{ вывод на экран вершин дерева /слева направо/ }
programm DisplayTree;
uses Crt;
type
TreePointer = ^tree
tree = record
data: char;
left: TreePointer;
right: TreePointer;
end;
var
root, dummy: TreePointer;
ch:char;
function STree(root, r:TreePointer; data: char):
TreePointer;
begin
if r = nil then
begin
new(r); { получить новую вершину }
r^.left := nil;
r^.right := nil;
r^.data := data;
if data < root^.data then root^.left := r
else root^.right := r;
STree := r;
end else
begin
if data<r^.data then STree := STree(r, r^.left, data)
else STree := STree(r, r^.right, data)
end;
end; { конец процедуры STree }
procedure PrintTree(r: TreePointer; n: integer);
var
i:integer;
begin
if r>nil then begin
PrintTree(r.^left, n+1);
for i := 1 to n do Write(' ');
Writeln(r^.data);
PrintTree(r^.right, n+1);
end;
end; { конец процедуры PrintTree }
begin
root := nil;
repeat
Write('enter a letter (Q to quit): ');
ch := ReadKey; Writeln(ch);
if root= nil then root := STree(root, root, ch)
else dummy := STree(root, root, ch);
ch := UpCase(ch);
until ch ='Q';
PrintTree(root, 0);
end;
В этой программе фактически делается сортировка полученной информации. В данном случае используется вариант сортировки вставкой. Для среднего случая сортировка вставкой имеет достаточно хорошие характеристики, однако быстрая сортировка все же является лучшим методом сортировки, так как она требует меньше оперативной памяти и выполняется быстрее. Однако, если дерево строится на основе использования других деревьев или если вам приходится поддерживать упорядоченное дерево, то новые элементы всегда будут вставляться с использованием функции STree.
Если вы воспользуетесь программой вывода на экран двоичного дерева, то возможно вы заметите, что некоторые деревья сбалансированы /т.е. все поддеревья имеют одинаковую или почти одинаковую высоту/, а другие сильно несбалансированы. Если вы введете дерево "abcd", то оно примет следующий вид:
a
\
\
b
\
\
c
\
\
d
В этом случае левых поддеревьев не будет. Это дерево называется вырожденным, поскольку оно выродилось в линейный список. В общем случае, если используемые для построения дерева данные являются в достаточной мере случайными, дерево будет приближаться к сбалансированному. Однако, если информация уже упорядочена, то в результате будет получаться вырожденное дерево. /Имеется возможность переупорядочивать дерево, сохраняя при каждой вставке его балансировку. Однако такой алгоритм достаточно сложен и если он вас заинтересовал, то следует воспользоваться книгами по усовершенствованным методам составления алгоритмов программ/.
Функции поиска для двоичных деревьев составляются легко. Ниже приводится функция, результатом которой является указатель на вершину дерева, которая совпадает с ключом. В противном случае возвращается нулевое значение.
{ поиск элемента в дереве }
function Search(root:TreePointer;
key:DataItem):TreePointer;
begin
if root <> nil
begin
while (root^.data <> key) and (root <> nil) do
begin
if key < root^.data then root := root^.left
else root := root^.right;
end;
end;
Search := root;
end; { конец процедуры поиска элемента }
К сожалению, удаление вершины дерева выполняется не так просто, как поиск вершины. Удаленной вершиной может быть корень, левая вершина или правая вершина. Вершина может также иметь от нуля до двух поддеревьев. Необходимость изменения указателей приводит, например, к следующему рекурсивному алгоритму .
{ удаление элемента из дерева }
function DTree(root:TreePointer;key:char):TreePointer;
var
temp,temp2:TreePointer;
begin
if root^.data = key then
begin
if root^.left=root^.right tnen
begin
dispose(root)
DTree := nil;
end
else if root^.left=nil tnen
begin
temp := root^.right
dispose(root)
DTree := temp;
end
else if root^.right=nil tnen
begin
temp := root^.left
dispose(root)
DTree := temp;
end
else
begin { имеются два листа }
temp2 := root^.right
temp := root^.right
while temp^.left <> nil do temp := temp^.left;
temp^.left := root^.left
dispose(root);
DTree := temp2
end;
else
begin
if root^.data < key
then root^.right := DTree(root^.right, key)
else root^.left := DTree(root^.left, key)
DTree := root;
end;
end; { конец функции DTree }
Следует помнить, что в основной программе необходимо обновлять указатель на корень дерева, так как удаленная вершина может оказаться корнем дерева.
Использование двоичных деревьев позволяет создавать мощные, гибкие и эффективные программы по управлению баз данных. Информация в этом случае может находиться на диске и поэтому важное значение может иметь время доступа. Число сравнений при использовании сбалансированных двоичных деревьев для худшего случая равно log2(n). Поэтому в этом случае поиск выполняется значительно быстрее, чем поиск в связанном списке, который посуществу является последовательным поиском.